
/es/sumar-y-restar/sumar-varios-numeros/content/
Conocer las propiedades de la suma te ayudará a comprender mejor esta operación. Además en algunos casos te servirán para simplificar tus cálculos.
En algunas ocasiones debemos sumar tres números o más. Si debemos hacer la suma , la propiedad asociativa nos asegura que podemos realizar esta operación de dos formas distintas obteniendo el mismo resultado, veamos:
Una de las formas es la siguiente: . En este caso los paréntesis nos indican que debemos sumar primeros los números: , luego el resultado de esta suma se opera con el tercer número, .
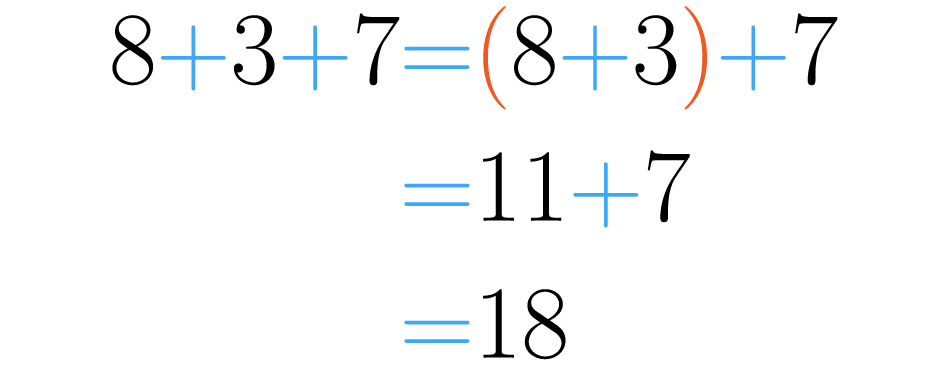
La otra forma es así: . Ahora los paréntesis nos dicen que primero debemos realizar la suma , una vez hecho esto podemos hacer la suma del primer número con el resultado obtenido en el paréntesis: .
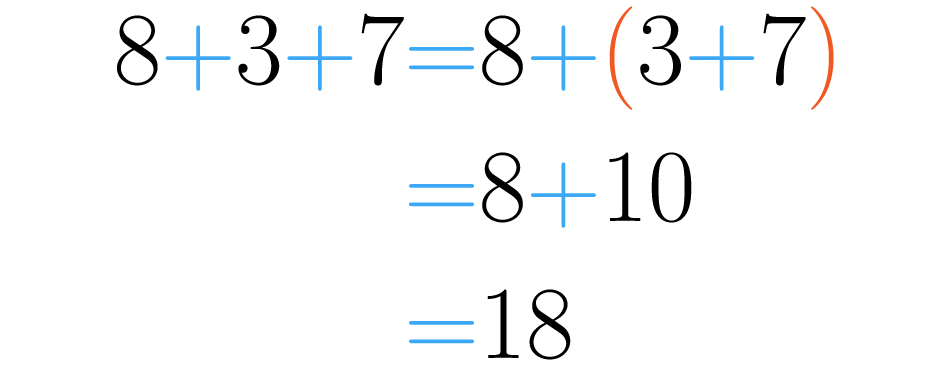
Como te puedes dar cuenta en ambos casos obtuvimos como resultado de la suma . Esto no sucede solo con los números ocho, tres y siete, ¡sucede con todos los números! Para generalizar esta idea podemos enunciar la propiedad asociativa así: dados tres números cualquiera y :
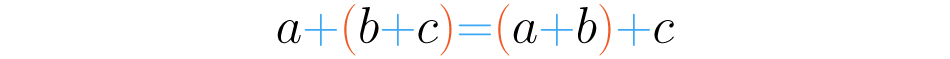
A través de los símbolos y estamos representando todos los números en general. La propiedad asociativa nos dice que cuando sumemos varios números, podemos asociarlos en el orden que más nos convenga.
¿Crees que el resultado de una suma cambia si cambiamos el orden de los sumandos? Por ejemplo, si realizamos las sumas y , ¿crees que los resultados serán distintos?
La propiedad conmutativa nos asegura que no importa el orden en que tomemos los sumandos, el resultado de la suma no cambiará. Puedes observar que y .
Igual que con la propiedad asociativa, esto se cumple para todos los números, podemos generalizar esta idea así: dados dos números y :
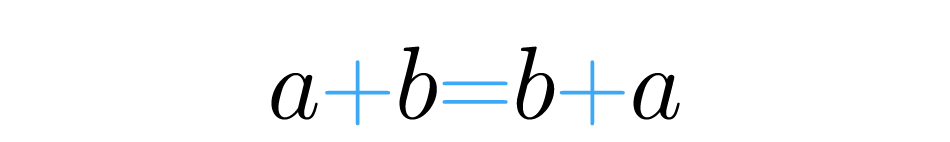
Esta propiedad es algo especial. Habla de la existencia de un número en particular que no afecta a los demás cuando se realiza la suma. ¿Conoces un número que sumado con uno, el resultado sea uno? ¿O que sumado con cincuenta, el resultado de la suma sea cincuenta? Pues un número así de especial para la suma sí existe, es nada más que el cero, . Fíjate:
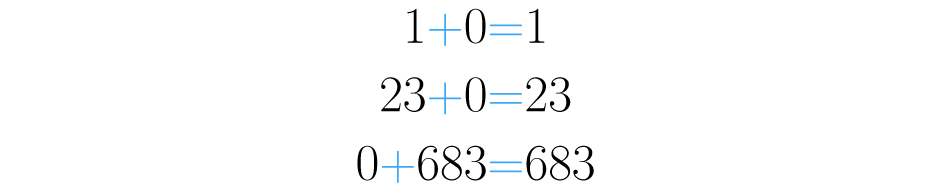
Y así podríamos seguir con todos los números.
Por eso se dice que el cero es el modulo de la suma, de hay el nombre de propiedad modulativa. Para generalizar esta idea podemos escribir: dado cualquier número se tiene:
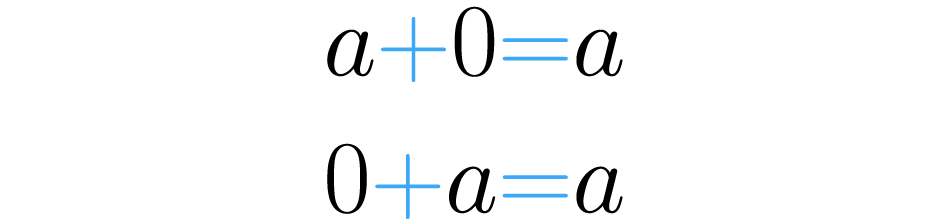
Para entender esta propiedad hace falta tener un conjunto de referencia, tomemos los números naturales. Una vez tenemos el conjunto de referencia, nos podemos preguntar si al sumar dos elementos de ese conjunto (dos números naturales), el resultado de la suma pertenece al mismo. Veamos:
Tomemos dos números naturales cualesquiera, por ejemplo y . La suma da como resultado , que también es un número natural.
Clausurar significa cerrar, por eso se dice también que la suma es cerrada sobre el conjunto de los naturales. Generalizando esta propiedad, se dice que si y son dos números naturales, entonces también lo es.
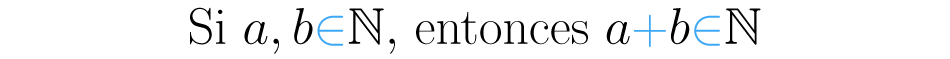
La suma también es clausurativa en los conjuntos de números enteros, racionales y reales, entre otros.
/es/sumar-y-restar/problemas-que-se-pueden-resolver-con-sumas/content/