Recursive partitioning

Recursive partitioning is a statistical method for multivariable analysis.[1] Recursive partitioning creates a decision tree that strives to correctly classify members of the population by splitting it into sub-populations based on several dichotomous independent variables. The process is termed recursive because each sub-population may in turn be split an indefinite number of times until the splitting process terminates after a particular stopping criterion is reached.

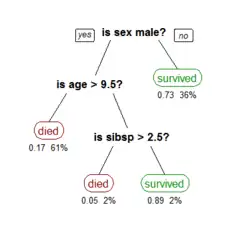
A recursive partitioning tree showing survival of passengers on the Titanic ("sibsp" is the number of spouses or siblings aboard). The figures under the leaves show the probability of survival and the percentage of observations in the leaf. Summarizing: Your chances of survival were good if you were (i) a female or (ii) a young boy without several family members.

Recursive partitioning methods have been developed since the 1980s. Well known methods of recursive partitioning include Ross Quinlan's ID3 algorithm and its successors, C4.5 and C5.0 and Classification and Regression Trees (CART). Ensemble learning methods such as Random Forests help to overcome a common criticism of these methods – their vulnerability to overfitting of the data – by employing different algorithms and combining their output in some way.

This article focuses on recursive partitioning for medical diagnostic tests, but the technique has far wider applications. See decision tree.

As compared to regression analysis, which creates a formula that health care providers can use to calculate the probability that a patient has a disease, recursive partition creates a rule such as 'If a patient has finding x, y, or z they probably have disease q'.

A variation is 'Cox linear recursive partitioning'.[2]

Advantages and disadvantages

Compared to other multivariable methods, recursive partitioning has advantages and disadvantages.

  • Advantages are:
    • Generates clinically more intuitive models that do not require the user to perform calculations.[3]
    • Allows varying prioritizing of misclassifications in order to create a decision rule that has more sensitivity or specificity.[2]
    • May be more accurate.[4]
  • Disadvantages are:
    • Does not work well for continuous variables[5]
    • May overfit data.

Examples

Examples are available of using recursive partitioning in research of diagnostic tests.[6][7][8][9][10][11] Goldman used recursive partitioning to prioritize sensitivity in the diagnosis of myocardial infarction among patients with chest pain in the emergency room.[11]

See also

  • Decision tree learning

References

  1. ↑ Breiman, Leo (1984). Classification and Regression Trees. Boca Raton: Chapman & Hall/CRC. ISBN 978-0-412-04841-8.
  2. 1 2 Cook EF, Goldman L (1984). "Empiric comparison of multivariate analytic techniques: advantages and disadvantages of recursive partitioning analysis". Journal of Chronic Diseases. 37 (9–10): 721–31. doi:10.1016/0021-9681(84)90041-9. PMID 6501544.
  3. ↑ James KE, White RF, Kraemer HC (2005). "Repeated split sample validation to assess logistic regression and recursive partitioning: an application to the prediction of cognitive impairment". Statistics in Medicine. 24 (19): 3019–35. doi:10.1002/sim.2154. PMID 16149128.
  4. ↑ Kattan MW, Hess KR, Beck JR (1998). "Experiments to determine whether recursive partitioning (CART) or an artificial neural network overcomes theoretical limitations of Cox proportional hazards regression". Comput. Biomed. Res. 31 (5): 363–73. doi:10.1006/cbmr.1998.1488. PMID 9790741.
  5. ↑ Lee JW, Um SH, Lee JB, Mun J, Cho H (2006). "Scoring and staging systems using cox linear regression modeling and recursive partitioning". Methods of Information in Medicine. 45 (1): 37–43. doi:10.1055/s-0038-1634034. PMID 16482368.
  6. ↑ Fonarow GC, Adams KF, Abraham WT, Yancy CW, Boscardin WJ (2005). "Risk stratification for in-hospital mortality in acutely decompensated heart failure: classification and regression tree analysis". JAMA. 293 (5): 572–80. doi:10.1001/jama.293.5.572. PMID 15687312.
  7. ↑ Stiell IG, Wells GA, Vandemheen KL, et al. (2001). "The Canadian C-spine rule for radiography in alert and stable trauma patients". JAMA. 286 (15): 1841–8. doi:10.1001/jama.286.15.1841. PMID 11597285.
  8. ↑ Haydel MJ, Preston CA, Mills TJ, Luber S, Blaudeau E, DeBlieux PM (2000). "Indications for computed tomography in patients with minor head injury". N. Engl. J. Med. 343 (2): 100–5. doi:10.1056/NEJM200007133430204. PMID 10891517.
  9. ↑ Edworthy SM, Zatarain E, McShane DJ, Bloch DA (1988). "Analysis of the 1982 ARA lupus criteria data set by recursive partitioning methodology: new insights into the relative merit of individual criteria". J. Rheumatol. 15 (10): 1493–8. PMID 3060613.
  10. ↑ Stiell IG, Greenberg GH, Wells GA, et al. (1996). "Prospective validation of a decision rule for the use of radiography in acute knee injuries". JAMA. 275 (8): 611–5. doi:10.1001/jama.275.8.611. PMID 8594242.
  11. 1 2 Goldman L, Weinberg M, Weisberg M, et al. (1982). "A computer-derived protocol to aid in the diagnosis of emergency room patients with acute chest pain". N. Engl. J. Med. 307 (10): 588–96. doi:10.1056/NEJM198209023071004. PMID 7110205.
This article is issued from Offline. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.