اكسنومتري كافاليرا

اكسنومتري كافاليرا (cavalier axonometry) هي نوع من الاكسنومتري المائلة التي تقوم على إسقاط نقاط جسم ما باتجاه مائل بالنسبة إلى مستوى الإسقاط π.

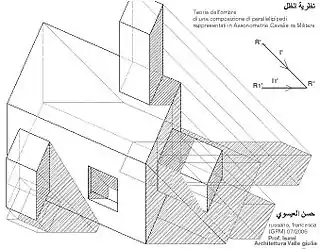
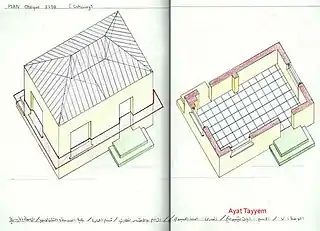
الاكسنومتري الكافاليرا الافقية (plan oblique)
مقطع لبيئة معمارية في الاكسنومتري الكافاليرا الافقية ( plan oblique cutaway)

الاكسنومتري الكافاليرا هكذا سميت بالنسبة إلى كافاليري بونافينتورا (Bonaventura Cavalieri)، عالم رياضيات متميز وطالب ل غاليليو غاليلي،

ميزة الاكسنومتري الكافاليرا هي أن الأشكال المستوية الموازية لمستوى الأسقاط π تبقى بشكلها ومقاسها الحقيقي بعد عملية الإسقاط، مثلاً الإسقاط الكافاليري 'Δ لدائرة Δ تنتمي إلى مستوى موازي π, هو دائرة لها نفس قطر الدائرة Δ.

هناك نوعان من الاكسنومتري الكافاليرا التي تصنف وفقا لمُوازاة أو تطابق أحد المستويات الإحداثية مع مستوى الاسقاط π وهما:

    • كافاليرا أفقيه ( Military Cavalier or Plan-obliques), عندما المستوى xy يوازي أو يتطابق مع π؛
    • كافاليرا رأسية (frontal Cavalier or Elevation-obliques), عندما تكون yz أو xz يوازي أو يتطابق مع π؛

كافاليرا أفقيه (plane oblique )
مثال للاكسونومتري كافاليرا أفقيه -(رسم 1

ميزة هذا النوع من الاكسنومتري هي أن الأشكال المستوية الأفقية تبقى بشكلها ومقاسها الحقيقي بعد عملية الإسقاط.

الاكسنومتري الكافاليرا الأفقية غالبا ما تستخدم لتسهيل عمليات تنفيذ الرسم التقليدي، الإجراء يكمن في دوران خطة مبنى ما بحيث تكون مثلاً 30 درجة بالنسبة لخط افقي الذي يمكن أن يكون حافة ورقة الرسم. ثم تُرسم الخطوط الرأسية التي تمثل ارتفاع المبنى. على سبيل المثال، عندما يكون مقياس الرسم 1:100 طول تلك الخطوط الرأسية ستكون 10 سم إذا كان ارتفاع المبنى يساوي 10 متر.

وعادة يُقلل مقاس الخطوط الرأسية (z//)، للحصول على رؤية قريبة من تلك المنظورية. على سبيل المثال، إذا نظرنا إلى مبنى من الأعلى نلاحظ ان ارتفاعه أقل من مقاس ارتفاعه الحقيقي. وبالمناسبة، عندما الصورة الكافاليرا الأفقية للارتفاع تساوي (بالتناسب) الارتفاع الحقيقي، وهذا يعني أن الزاوية بين اتجاه ومستوى الإسقاط تساوي 45 درجة؛ وهذه هي القيمة الأدنى التي يمكنك استخدامها. أي أن مقاسات الارتفاعات يمكن أن تساوي تلك الحقيقية أو ان تقلل حسب الاختيار. للتبسيط عادة ما يختار النصف كعامل تقليل للارتفاعات.

مثال

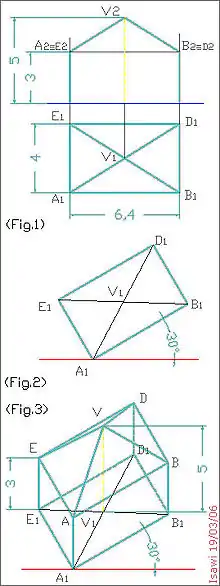
ليكن لدينا البيانات التالية (رسم 1):

  • الإسقاط المونجي لموازي سطوح قائم K، القاعدة المستطيلة العلوية لK هي أيضاً القاعدة لهرم قائم R. يريد رسم الاكسنومتري الكافاليرا لتلك الأحجام (Fig.1.[1]

الإجراء
  1. نرسم القاعدة المستطيلة A1B1C1D1 بحيث يكون الضلع A1B1 دائر ب30 درجة، كما يظهر في الرسمة (Fig.2).
  2. من الرؤوس A1B1C1D1 نرسم بالتوالي الخطوط الرأسية التي تمثل احرف موازي السطوح K كما هو مبين في الرسم Fig.3
  3. على الخطوط الرأسية نحدد ارتفاع K بنفس المقاس الذي يؤخذ من المسقط المونجي الثاني للمنشور K، وبهذه الطريقة يتم تحديد القاعدة العلوية ABCD للمنشور K.
  4. من المسقط الأول V1 (كما هو مبين في الرسم:fig.3) لرأس الهرم R نرسم خط رأسي مستقيم الذي يمثل محور الهرم؛
  5. على هذا المحور نحدد ارتفاع الهرم وهكذا نجد رأس الهرم V؛
  6. وأخيراً, نوصل رؤوس القاعدة ABCD مع V لنجد احرف الهرم R.

كافاليرا رأسية (cabinet )
كافاليرا رأسية

ميزة هذا النوع من الاكسنومتري هي أن الأشكال المستوية الأمامية (عندما يكون π // yz)، أو الجانبية (عندما يكون π // xz) تبقى بشكلها ومقاسها الحقيقي بعد عملية الإسقاط. البعد الثالث الذي يمكن ان يكون y (أو x) يمكن ان يبقى بمقاسه الحقيقي, أو من الأفضل تقليل, ذلك المقاس, بأي نسبة مختارة, مثلاً النصف.

سبب هذا التقليل هو ان مركز الإسقاط ,في الإسقاط الاكسنومتري بشكل عام, يوجد في نقطة لانهائية ولهذا فهو يمثل وضع غير طبيعي بالنسبة للتصور الإنساني. ولذلك، تقليل البعد الثالث الذي يمثل الارتفاع في الكافاليرا الأفقية والعمق في الكافاليرا الرأسية, هي محاولة تهدف إلى تقريب التصور الاكسنومتري إلى المنظوري.

معرض
  • قطاع اكسنومتري. كافاليرا أفقيه (plane oblique)

مصادر
  1. Assonometria Cavaliera militare نسخة محفوظة 07 ديسمبر 2017 على موقع واي باك مشين.
  • بوابة فنون مرئية
  • بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.