البحث المتسع الاول

بيانات عامّة
الصنف	uninformed search algorithm (en) — graph traversal (en)
بنية البيانات	بيان
المكتشف	كونراد سوزه
تاريخ الاكتشاف	1945
أسوء حالة
أسوأ حالة تعقيد مكاني

بحث اتساعي الأولوية / افقي الأولوية أو البحث المتوسع والمسمى أيضا خوارزمية BFS[1] هي العملية التي تقوم بالمرور المنهجي من جميع الرؤوس في بيان (G(V،E وترقيمها حسب ترتيب الزيارة، عبورا بالحواف الموجودة داخل المكونات المتصلة للبيان. تتم زيارة كل رأس في (G(V،E مرة واحدة.

كيفية العمل

بدءًا من أي رأس (v∈V(G ، تتم زيارة جميع الرؤوس المجاورة لالرأس v أولاً، ثم الرؤوس المجاورة لكل من الرؤوس المجاورة لالرأس v ، أي الرؤوس على مسافة حافتين نسبة إلى v ، وهلم جرا.

لكي يكون ترتيب زيارة الرؤس متسقًا مع وصفها النظري، فإن خوارزمية BFS عبارة عن مخطط تكراري مبني حول طابور Q ، يمثل البنية البيانية المركزية للانغراز العملي للخوارزمية، وهي نظريّا مجموعة مرتّبة يتم فيها إدخال العناصر من «الذيل» ونزعها من «الرأس»، وبهذا الشكل أوّل عنصر يضاف إلى Q هو أول من يخرج منها مع حفاظ ترتيب كل العناصر الموجودة في القائمة.

في كل تكرار تتم زيارة موجة من الرؤوس متساوية المسافة من v ، ونرى أنها تنتشر خلال العملية، حتى يتم زيارة جميع الرؤوس في البيان التي يمكن الوصول إليها من v.

تعاد هذه العملية لكل المكونات المتصلة في البيان (G(V،E

خوارزمية BFS

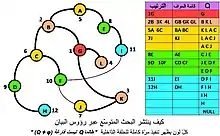
ضع علامة 0 على كل رؤوس (G(V،E

قائمة الحواف A ← φ (مجموعة فارغة)

طابور الزيارات Q ← φ (مجموعة فارغة)

C ← 1

طالما علامة رأس v هي 0

C ← علامة الرأس v

1+C ← C

{Q ← Q ∪ {v

طالما Q ليست فارغة (Q ≠ φ)

لجميع الرؤوس u_i المجاورة لـ v₀ وهو الرأس الأول في Q

إذا u_i له علامة 0

C ← علامة u_i

1+C ← C

ضف (v_o،u_i) إلى قائمة الحواف A

{Q ← Q ∪ {u_i

نهاية إذا

نهاية لجميع

{Q ← Q - {v₀ (حدف الرأس الأول من الطابور Q)

نهاية طالما

الخصائص والتطبيقات

عدد المكونات المتصلة في البيان (G(V،E هو عدد مرات تنفيذ الحلقة الخارجية «طال ما علامة رأس v هي 0» في الخوارزنية
يصلح استعمال BFS في كل بيان بغض النظر سواء كان البيان موجها أم لا
تشكل الحواف التي تم عبورها بواسطة BFS شجرة مسارات أقصر مسافات بين رأس الانطلاق (و هو جذر الشجرة) وجميع الرؤوس الأخرى في (G(V،E. المسافة هنا تقدّر بعدد الحواف التي تكوّن المسار.

لخوارزمية BFS العديد من التطبيقات، معظمها كروتين أولية في الخوارزميات ذات أكثر تعقيد المألوفة في نظرية البيانات والتدفق في الشبكات، والأكثر استخداما من بينها هي:

الكشف عن حلقة في بيان موجه (G(V،A
اختبار استوائبة البيان (G(V،E[2]
خوارزميات اختبار الوصول أو مسألة المجاورة المتعدية[3] ، وهي امكانية الانتقال من رأس إلى آخر في البيان عبر الحواف الموجودة

انظر أيضا

مراجع

TARJAN, Robert Endre. Data structures and network algorithms. Siam, 1983.
HOPCROFT, John et TARJAN, Robert. Efficient planarity testing. Journal of the ACM (JACM), 1974, vol. 21, no 4, p. 549-568.
AHO, Alfred V. , GAREY, Michael R., et ULLMAN, Jeffrey D. The transitive reduction of a directed graph. SIAM Journal on Computing, 1972, vol. 1, no 2, p. 131-137.

بوابة علم الحاسوب
بوابة رياضيات

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] TARJAN, Robert Endre. Data structures and network algorithms. Siam, 1983.

[2] HOPCROFT, John et TARJAN, Robert. Efficient planarity testing. Journal of the ACM (JACM), 1974, vol. 21, no 4, p. 549-568.

[3] AHO, Alfred V. , GAREY, Michael R., et ULLMAN, Jeffrey D. The transitive reduction of a directed graph. SIAM Journal on Computing, 1972, vol. 1, no 2, p. 131-137.