جريان صفيحي

بغرض التفرقة بين جريان صفيحي لسائل و جريان مضطرب قام الفيزيائي «أوزبورن رينولدز» في عام 1883 بإجراء تجارب على الماء مع استخدام ألوان يمكن بواسطتها رؤية سريان الماء وانسيابه الهاديء أو نشأة دوامات فيه . وباستخدامه أنبوب زجاجي يدع الماء يجرى فيه، اتضح له أن الماء في الأنبوب يبدأ الاضطراب وتولد دوامات فيه عندما تصل سرعة الماء (أو السائل أو المائع) سرعة معينة . وقد صاغ نتائجه كدالة يدخل فيها عدد رينولد Re ، ويعرف عدد رينولد بالمعادلة الآتية:

${\displaystyle \mathrm {Re}$ :={\frac {v\cdot l}{\nu }}={\frac {v\cdot l\cdot \rho }{\mu }}} ,

تكون طبقة صفيحية على سطح مسطح . Re_x اصغر من Re_krit ≈ 10⁵ لكل قيمة من x التي هي طول السطح ، ويجب أن تكون لها قيمة .

حيث:

${\displaystyle v}$ سرعة جريان خاصة للمائع

${\displaystyle l}$ طول خاص للسطح

${\displaystyle \nu }$ اللزوجة الكينماتية للمائع أو ${\displaystyle \mu }$ أو (${\displaystyle \eta }$ اللزوجة الحركية)

${\displaystyle \rho }$ كثافة المائع الجاري.

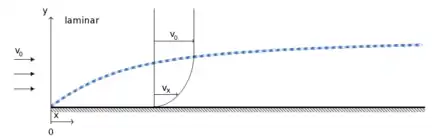
الشكل إلى اليسار:

الشكل يوضح أن الماء الجاري على سطح مسطح يتكون من طبقات رقيقة فوق بعضها (الاتجاه y) (طول السطح هو x ). الطبقة الملامسة للسطح الصلب تبلغ سرعتها صفر (لا حركة) . تليها طبقة ماء ذات سرعة صغيرة، وتتلوها طبقة ثالثة أسرع من سابقتها، وهكذا . فإذا كان سريان المائع في أنبولب، تكون طبقة المائع الجاري الملامسة للسطح الداخلي للأنبوب ثابتة مستقرة . وتزداد سرعة طبقات الماء في اتجاه منتصف الأنبوب (محور الأنبوب الأسطواني).

عندما تصل Re إلى القيمة الحرجة ${\displaystyle \mathrm {Re_{krit}} }$ وفوقها تبدأ حركة اضطرابية في المائع بسبب أي اختلال صغير . وعلى سبيل المثال: تبلغ هذه القيمة الحرجة داخل أنبوب :

${\displaystyle \mathrm {Re_{krit}} ={\frac {v_{\mathrm {m} }\cdot d}{\nu }}\approx 2320}$

حيث:

${\displaystyle v_{m}}$ متوسط سرعة جريان المائع,

${\displaystyle d}$ قطر الأنبوب.

وفي حالة جريان مائع على سطح مستوي تكون قيمة العدد الحرج :

${\displaystyle \mathrm {Re_{krit}} ={\frac {v_{0}\cdot x}{\nu }}\approx 10^{5}}$.

حيث:

${\displaystyle x}$ طول السطح من أوله إلى آخره،

و ${\displaystyle v_{0}}$ سرعة اجريان المائع .

في حالة سريان صفيحي لمائع في أبوب، فيمكن أيضا تطبيق قانون هاجن-بوازوي. وهو يصف حجم الجريان ${\displaystyle {\tfrac {\mathrm {d} V}{\mathrm {d} t}}}$ داخل أنبوب كدالة لنصف قطر الأنبوب.

• جريان مضطرب
• جريان ستوكس
• طبقة حدية
• عدد ستروهال
• عدد رينولد
• شارع كارمان الدوامي
• قانون هاجن-بوازوي
• معادلة السحب
• مقياس اللزوجة

• بوابة هندسة ميكانيكية
• بوابة الفيزياء