خطوط طيف الهيدروجين

خطوط طيف الهيدروجين ينقسم طيف انبعاث ذرات الهيدروجين إلى عدة مجموعات أطياف، وتعطي معادلة ريدبرج أطوال موجاتها. تنشأ تلك الخطوط الطيفية من انتقال الإلكترون في ذرة الهيدروجين بين مستويات طاقة مختلفة. وتستخدم مسلسلات أطياف بصفة خاصة في علم الفلك بغرض التعرف على أماكن وجود الهيدروجين في الكون، وكذلك في حساب الانزياح الأحمر الذي نرصده في الأجرام السماوية البعيدة عنا. كذلك اكتشفت عدة أطياف أخرى بتقدم تقنية المطيافية.

خطوط طيف الهيدروجين: توضيح المتسلسلات.

مسلسلات خطوط طيف الهيدروجين، بمقياس رسم لوغاريتمي.

يختلف طيف الهيدروجين عن أطياف العناصر الكيميائية الأخرى، مثل الكربون والأكسجين والحديد وغيرها، أي يختلف توزيع خطوط الطيف التي نستطيع قياسها معمليا عند تسخين أو إشعال العينة، وتوزيعها يعطينا نوع عنصر العينة، إذ لكل عنصر "بصمة" من خطوط الطيف خاصة به. ويستغل التحليل الطيفي في الكيمياء لمعرفة مكونات عينة من العناصر (أنظر مطيافية).

فيزياء

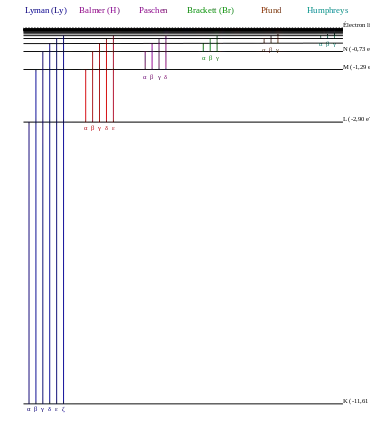
يفسر ظهور خطوط طيف الهيدروجين بقفزات معينة للإلكترون بين مستويات الطاقة لذرة الهيدروجين. وأبسط نموذج لذرة الهيدروجين يعطيه نموذج بور الذي اقترحه العالم الدانمركي نيلز بور عام 1913 . طبقاً لهذا النموذج، عندما يقفز الإلكترون من مستوى طاقة عالي إلى مستوى طاقة منخفض فإنه يُصدر فوتونا له طول موجة معينة.

انتقالات الإلكترون بين مستويات الطاقة المختلفة وأطوال موجة الضوء الناتجة عنها
. مجموعة خطوط لايمان : انتقالات إلى n=1 .
. مجموعة خطوط بالمر: انتقالات إلى مدار n=2 .
. مجموعة خطوط باشين : انتقالات إلى المدار n=3 ...الخ

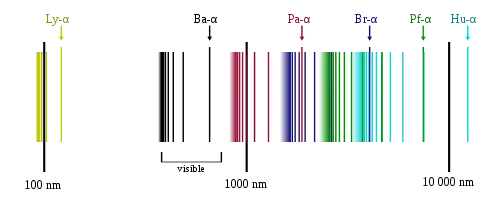
تجمع خطوط الطيف في مجموعات أو مسلسلات. وتبدأ كل مجموعة بالخط ذو أطول موجة(أو أقل تردد) فيها. وتستخدم لها حروفا يونانية تعبر عن كل مسلسلة. وعل سبيل المثال: الخط 2 ← 1 يسمى "لايمان-ألفا" Ly-α، بينما الخط 7 ← 3 فيسمى "باشين-دلتا" Pa-δ . وبعض خطوط طيف الهيدروجين تقع خارج تلك المسلسلات، مثل خط الهيدروجين ذو طول الموجة 21 سنتيمتر. ولكن مثل هذا الخط يحدث عن انتقالات نادرة للإلكترون في ذرة الهيدروجين، ويسمى هذا الانتقال "انتقال بنية فائقة الدقة. [1] كذلك تؤدي البنية الدقيقة للذرة إلى خطوط طيف تظهر مزدوجة أو أكثر من خطين تكون قريبة من بعضها جداً، وهي ناشئة عن تأثيرات النظرية النسبية على الإلكترون (أي بسبب سرعات للإلكترون قريبة من سرعة الضوء في الذرة). [2]

نستطيع رؤية تلك الخطوط في طيف الهيدروجين في المختبر عندما تكون العينة نقية. وبعض تلك الخطوط يكون خافتا، ويمكن أن يختلط بخطوط من عناصر أخرى (مثل خطوط الهيليوم إذا استخدمنا ضوء الشمس، أو خطوط النيتروجين إذا كان التحليل في الهواء). أما الخطوط خارج الطيف المرئي فهي لا يمكن رؤيتها في ضوء الشمس حيث أن جو الأرض يمتص معظم أطوال موجات الأشعة تحت الحمراء والأشعة فوق البنفسجية.

معادلة ريدبرج

تعطي معادلة ريدبرج فرق الطاقة بين مستويين في نموذج بور لذرة الهيدروجين، وبذلك تعطي أطوال الموجات الضوئية (فوتون الصادرة من الذرة أو الممتصة فيها.

[3]

{1 \over \lambda }=R\left({1 \over (n)^{2}}-{1 \over (n^{\prime })^{2}}\right)\qquad \left(R=1.097373\times 10^{7}\ \mathrm {m} ^{-1}\right)

حيث:

n مستوى الطاقة الباديء منه الإلكترون،

n' مستوي الطاقة النهائي،

R ثابت ريدبرج.[4]

تعطي تلك المعادلة قيما حقيقية عندما تكون n أكبر من n'.

المسلسلات

تنتسب كل مجموعة أو مسلسلة من خطوط الطيف إلى المدار التحتي الذي يقفز إليه الإلكترون في ذرة الهيدروجين. فمثلا مجموعة خطوط لايمان تتم قفزات الإلكترون فيها إلى المدار رقم 1 . أما مجموعة بالمر مثلا فجميعها قفزات للإلكترون من أعلى إلى المدار رقم 2 (أنظر الصورة)، وهكذا.

مجموعة لايمان (n′ = 1)

((n)	λ (nm
2	122
3	103
4	97.3
5	95.0
6	93.8
$\infty$	91.2

مجموعة خطوط لايمان لذرة الهيدروجين في نطاق الأشعة فوق البنفسجية.

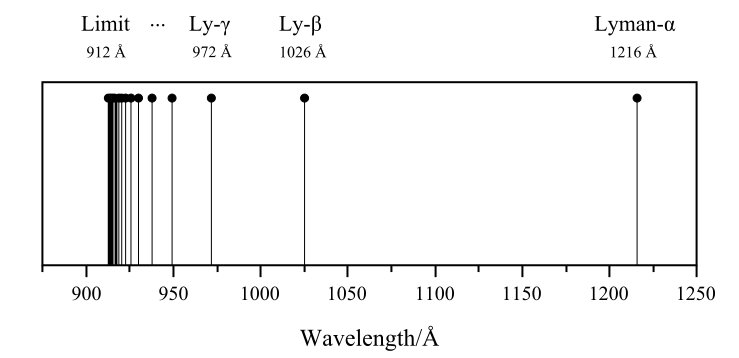
سميت تلك المسلسلة باسم مكتشفها ثيودور لايمان الذي اكتشف خطوط الطيف بين 1906 إلى 1914 . جميع خطوط مجموعة لايمان توجد في نطاق الأشعة فوق البنفسجية. [5][6]

مجموعة خطوط بالمر (n′ = 2)

(n)	λ (nm)
3	656
4	486
5	434
6	410
7	397
$\infty$	365

تسمى مجموعة الخطوط هذه باسم مكتشفها يوهان بالمر الذي اكتشف معادلة بالمر معمليا وقام بصياغة المعادلة على أساس ما قام بقياسه بالمختبر. كان ذلك في عام 1885 . ويرمز إلى خطوط بالمر بالرموز: "إتش-ألفا" و، "H-beta" و، "H-gamma"....وهكذا، حيث ترمز H إلى الهيدروجين.[7]

أربعة خطوط من خطوط بالمر تظهر في نطاق الضوء المرئي بأطوال موجة أطول من 400 نانومتر وأقصر من 700 نانومتر. وبعض خطوط بالمر يمكن رياها أيضا في طيف الشمس. ويتبوأ خط H-alpha مركزا هاما في علم الفلك حيث يستخدم لاكتشاف الهيدروجين.

الأربعة خطوط المرئية في مجموعة بالمر .الخط H-alpha هو الخط الأحمر إلى اليمين.

مجموعة خطوط باشين (مسلسلة بور) (n′ = 3)

(n)	λ (nm)
4	1870
5	1280
6	1090
7	1005
8	954
$\infty$	820

تسمى تلك المجموعة باسم مكتشفها العالم النمساوي الألماني "فريدريش باشين"، وقد اكتشفها في عام 1908. تقع جميع خطوط مجموعة باشين في حيز الأشعة تحت الحمراء، أي أننا لا نستطيع رؤياها بالعين المجردة، ولكن توجد كاميرات لتصويرها. [8]

مجموعة خطوط براكيت (n′ = 4)

(n)	λ (nm)
5	4050
6	2620
7	2160
8	1940
9	1820
$\infty$	1460

تسمى تلك المجموعة باسم مكتشفها الفيزيائي الأمريكي "فريدريك براكيت" وقد اكتشفها في عام 1922. [9]

مجموعة خطوط بفوند (n′ = 5)

(n)	λ (nm)
6	7460
7	4650
8	3740
9	3300
10	3040
$\infty$	2280

اكتشفها الفيزيائي "أوجوست بفوند" عام 1924 . [10]

مجموعة خطوط همفريز (n′ = 6)

(n)	λ (nm)
7	12400
8	7500
9	5910
10	5130
11	4670
$\infty$	3280

واكتشفها الفيزيائي الأمريكي "كورتيس همفريز" وقام بنشرها في عام 1953 . [11]

مجموعات خطوط بعد المدار (n′ > 6)

توجد أيضا مجموعات خطوط طيف تنتهي عند مدارات في ذرة الهيدروجين أعلى من 6 . وهي تتبع نفس النموذج الذي تحدده معادلة ريدبرج. تتباعد الخطوط فيها وتزداد فيها أطوال الموجات. كما تضعف شدة الخطوط مما يعني أن انتقالات الإلكترون التي يصدرها تصبح نادرة.

تطبيق على أنظمة أخرى

يمكن تطبيق معادلة ريدبرج عل انظمة أخرى لها إلكترون واحد يدور حول النواة، مثل أيون He⁺ أو ذرة ميونيوم الغريبة. في تلك الأنظمة يجب تعديل المعادلة بالنسبة إلى نصف قطر بور، فتكون الإصدارات الفوتونات بنفس المنظومة لكن سيختلف حيز طاقاتها عن تلك المعروفة للهيدروجين.

أما الذرات الأخرى فهي تحوي إلكترونين أو أكثر والتآثر بين الإلكترونات يجعل تحليل طيف تلك الذرات غير عمليا. وقد كان استنباط معادة ريدبرج عملا عظيما في الفيزياء، واستنبطت قبل دراسة أطياف العناصر التي تحتوي على إلكترونين أو أكثر.

في نفس الوقت تأيد معادلة ريدبرج واستنتاجها لمسلسلة طيف الهيدروجين أن معلوماتنا عن ذرة الهيدروجين صحيحة، وخصوصا وأن نظرية الكم تبعه ابتكار الفزيائيين لميكانيكا الكم التي تصف ذرة الهيدروجين وسلوك الإلكترون فيها وصفا دقيقا. ومن المعروف أن هايزنبرج الذي يرجع إليه ابتكار ميكانيكا الكم قد قام بذلك مبتدءا بطيف الهيدروجين، وحل المسألة بطريقة المصفوفات حيث تؤدي بعض عناصر المصفوف إلى إصدار فوتونا أما الأخرى فلا ينتج منها إصدار فوتون.

انظر أيضا

المراجع

"The Hydrogen 21-cm Line"، هايبرفيزيكس، جامعة ولاية جورجيا، 30 أكتوبر 2004، مؤرشف من الأصل في 29 يوليو 2018، اطلع عليه بتاريخ 18 مارس 2009.
Liboff, Richard L. (2002)، Introductory Quantum Mechanics، Addison-Wesley، ISBN 0-8053-8714-5.
Bohr, Niels (1985)، "Rydberg's discovery of the spectral laws"، في Kalckar, J. (المحرر)، N. Bohr: Collected Works، Amsterdam: North-Holland Publ.، ج. 10، ص. 373–9
"CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF)، Committee on Data for Science and Technology (CODATA)، المعهد الوطني للمعايير والتقنية، مؤرشف من الأصل (PDF) في 12 يونيو 2018.
Lyman, Theodore (1906)، "The Spectrum of Hydrogen in the Region of Extremely Short Wave-Length"، Memoirs of the American Academy of Arts and Sciences، New Series، 13 (3): 125–146، ISSN 0096-6134، JSTOR 25058084
Lyman, Theodore (1914)، "An Extension of the Spectrum in the Extreme Ultra-Violet"، Nature، 93: 241، Bibcode:1914Natur..93..241L، doi:10.1038/093241a0
Balmer, J. J. (1885)، "Notiz uber die Spectrallinien des Wasserstoffs"، Annalen der Physik، 261 (5): 80–87، Bibcode:1885AnP...261...80B، doi:10.1002/andp.18852610506، مؤرشف من الأصل في 18 ديسمبر 2019
Paschen, Friedrich (1908)، "Zur Kenntnis ultraroter Linienspektra. I. (Normalwellenlängen bis 27000 Å.-E.)"، Annalen der Physik، 332 (13): 537–570، Bibcode:1908AnP...332..537P، doi:10.1002/andp.19083321303، مؤرشف من الأصل في 10 يناير 2020
Brackett, Frederick Sumner (1922)، "Visible and infra-red radiation of hydrogen"، Astrophysical Journal، 56: 154، Bibcode:1922ApJ....56..154B، doi:10.1086/142697
Pfund, A. H. (1924)، "The emission of nitrogen and hydrogen in infrared"، J. Opt. Soc. Am.، 9 (3): 193–196، doi:10.1364/JOSA.9.000193
Humphreys, C.J. (1953)، "Humphreys Series"، J. Research Natl. Bur. Standards، 50

بوابة الفيزياء
بوابة كيمياء فيزيائية
بوابة الكيمياء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "The Hydrogen 21-cm Line"، هايبرفيزيكس، جامعة ولاية جورجيا، 30 أكتوبر 2004، مؤرشف من الأصل في 29 يوليو 2018، اطلع عليه بتاريخ 18 مارس 2009.

[2] Liboff, Richard L. (2002)، Introductory Quantum Mechanics، Addison-Wesley، ISBN 0-8053-8714-5.

[3] Bohr, Niels (1985)، "Rydberg's discovery of the spectral laws"، في Kalckar, J. (المحرر)، N. Bohr: Collected Works، Amsterdam: North-Holland Publ.، ج. 10، ص. 373–9

[CODATA-4] "CODATA Recommended Values of the Fundamental Physical Constants: 2006" (PDF)، Committee on Data for Science and Technology (CODATA)، المعهد الوطني للمعايير والتقنية، مؤرشف من الأصل (PDF) في 12 يونيو 2018.

[5] Lyman, Theodore (1906)، "The Spectrum of Hydrogen in the Region of Extremely Short Wave-Length"، Memoirs of the American Academy of Arts and Sciences، New Series، 13 (3): 125–146، ISSN 0096-6134، JSTOR 25058084

[6] Lyman, Theodore (1914)، "An Extension of the Spectrum in the Extreme Ultra-Violet"، Nature، 93: 241، Bibcode:1914Natur..93..241L، doi:10.1038/093241a0

[7] Balmer, J. J. (1885)، "Notiz uber die Spectrallinien des Wasserstoffs"، Annalen der Physik، 261 (5): 80–87، Bibcode:1885AnP...261...80B، doi:10.1002/andp.18852610506، مؤرشف من الأصل في 18 ديسمبر 2019

[8] Paschen, Friedrich (1908)، "Zur Kenntnis ultraroter Linienspektra. I. (Normalwellenlängen bis 27000 Å.-E.)"، Annalen der Physik، 332 (13): 537–570، Bibcode:1908AnP...332..537P، doi:10.1002/andp.19083321303، مؤرشف من الأصل في 10 يناير 2020

[9] Brackett, Frederick Sumner (1922)، "Visible and infra-red radiation of hydrogen"، Astrophysical Journal، 56: 154، Bibcode:1922ApJ....56..154B، doi:10.1086/142697

[10] Pfund, A. H. (1924)، "The emission of nitrogen and hydrogen in infrared"، J. Opt. Soc. Am.، 9 (3): 193–196، doi:10.1364/JOSA.9.000193

[11] Humphreys, C.J. (1953)، "Humphreys Series"، J. Research Natl. Bur. Standards، 50