دالة متعددة المتغيرات الحقيقية

في التحليل الرياضي، دالة ذات عدة متغيرات هي دالة نطاقها مجموعة جزئية من $\mathbb {R} ^{n}$ حيث n>1
.[1] حيث تمثل الدالة في فضاء ثلاثي الأبعاد بحيث يكون الإحداثي العمودي للنقطة هو قيمة الدالة عند العنصر الممثل بالاحداثين الأولين، وهذا التمثيل يسمى «السطح الممثل للدالة». مجموعة التعريف لدالة ذات n متغير، هي مجموعة مشتقة من $\mathbb {R} ^{n}$ و مدى هذه الدالة هي مجموعة مشتقة من $\mathbb {R}$ بعض الدوال تكون معرفة لجميع الأعداد الحقيقية $R^{n}$ ، ولكن البعض الآخر تكون معرفة لمجموعة مشتقة من $\mathbb {R} ^{n}$

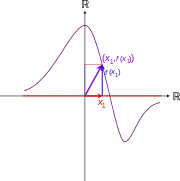
n = 1

n = 2

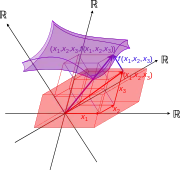
n = 3

الدوال

f (x 1, x 2, ..., x n)

لـ

n

متغير، مرسومة كرسومات بيانية في الفضاء

ℝ n + 1

. المجالات هي المناطق n-الأبعاد الحمراء، والصور هي منحنيات n-الأبعاد ذات اللون الأرجواني.

تعريف السطح الممثل لدالة

لتكن $f:A\rightarrow \mathbb {R} ^{2}$ حيث A مجموعة جزئية من $\mathbb {R} ^{2}$ ، السطح الممثل للدالة f هو مجموعة النقاط.

G(f)=\{(x,y,z)\in \mathbb {R} ^{3}|(x,y)\in A\ \ {\text{and}}\ \ z=f(x,y)\}

وبالمثل إذا كانت $f:A\rightarrow \mathbb {R} ^{3}$ حيث A مجموعة جزئية من $\mathbb {R} ^{3}$ فإن مجموعة النقاط

G(f)=\{(x,y,z,t)\in \mathbb {R} ^{3}|(x,y,z)\in A\ \ {\text{and}}\ \ z=f(x,y,z)\}

تسمى التمثيل البياني للدالة.

انظر أيضا

مراجع

"معلومات عن دالة متعددة المتغيرات الحقيقية على موقع id.loc.gov"، id.loc.gov، مؤرشف من الأصل في 26 أكتوبر 2020.

وصلات خارجية

بوابة تحليل رياضي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "معلومات عن دالة متعددة المتغيرات الحقيقية على موقع id.loc.gov"، id.loc.gov، مؤرشف من الأصل في 26 أكتوبر 2020.