سي 3 الخطية (خوارزمية)

في الحوسبة، (بالإنجليزية: C3 linearization)‏ خطية الطبقة الفائقة C3 هي خوارزمية تُستخدم في المقام الأول للحصول على الترتيب الذي يجب أن تتوارث فيه الطرق في وجود وراثة متعددة. بعبارة أخرى، ناتج خطي الطبقة الفائقة C3 هو أمر قرار حتمي للطريقة (MRO).

ينتج عن خطي الطبقة الفائقة C3 ثلاث خصائص مهمة:

  • رسم بياني متسق للأسبقية الموسعة،
  • الحفاظ على ترتيب الأسبقية المحلي، و
  • تلائم معيار الرتابة.

تم نشره لأول مرة في مؤتمر OOPSLA لعام 1996 ، في ورقة بعنوان «خطية أحادية الطبقة فائقة المستوى لديلان». تم تكييفه مع تطبيق Open Dylan في يناير 2012 [1] بعد اقتراح تحسين. [2] تم اختيارها كخوارزمية افتراضية لتحليل الأسلوب في بايثون 2.3 (وأحدث) ، [3] [4] Raku ، [5] Parrot ، [6] ، Solidity ، وPGF / TikZ للبرمجة الموجهة للكائنات.[7] يتوفر أيضًا كبديل غير افتراضي MRO في جوهر بيرل 5 بدءًا من الإصدار 5.10.0. [8] يوجد تطبيق ملحق للإصدارات السابقة من بيرل 5 باسم Class::C3 على CPAN . [9]

يلخص جويدو فان روسوم بايثون خطية الطبقة الفائقة C3 بالتالي: [10]

«Basically, the idea behind C3 is that if you write down all of the ordering rules imposed by inheritance relationships in a complex class hierarchy, the algorithm will determine a monotonic ordering of the classes that satisfies all of them. If such an ordering can not be determined, the algorithm will fail.»

وصف

إن الخطية الخطية للصنف الفائق C3 للصنف هي مجموع الأصناف بالإضافة إلى دمج فريد من الخطية لأبويها وقائمة بالآباء أنفسهم. تحافظ قائمة الآباء باعتبارها الوسيطة الأخيرة لعملية الدمج على ترتيب الأسبقية المحلي للفئات الرئيسية المباشرة.

يتم دمج قائمة الوالدين الخطية وقائمة الآباء عن طريق اختيار العنوان الأول للقوائم التي لا تظهر في الذيل (جميع عناصر القائمة باستثناء الأول) لأي من القوائم. لاحظ أن الرأس الجيد قد يظهر كعنصر أول في قوائم متعددة في نفس الوقت، لكن يحظر الظهور في أي مكان آخر. تتم إزالة العنصر المحدد من جميع القوائم حيث يظهر كرأس ويتم إلحاقه بقائمة الإخراج. تتكرر عملية اختيار وإزالة رأس جيد لتوسيع قائمة المخرجات حتى يتم استنفاد جميع القوائم المتبقية. إذا لم يتم تحديد رأس جيد في وقت ما، لأن رؤوس جميع القوائم المتبقية تظهر في أي ذيل واحد من القوائم، فمن المستحيل حساب الدمج بسبب الترتيب غير المتسق للتبعيات في التسلسل الهرمي للميراث وعدم وجود خطي للقوائم الأصلية فئة موجودة.

قد يستدعي نهج فرق تسد ساذج لحساب التحويل الخطي لفئة ما الخوارزمية بشكل متكرر للعثور على الخطية للأصناف الرئيسية لروتين الدمج الفرعي. ومع ذلك، سينتج عن ذلك تكرار متكرر لا نهائي في وجود تسلسل هرمي للصنف الدوري. لاكتشاف مثل هذه الدورة وكسر العودية اللانهائية (وإعادة استخدام نتائج الحسابات السابقة كتحسين)، يجب حماية الاستدعاء العودي من إعادة إدخال وسيطة سابقة عن طريق ذاكرة التخزين المؤقت أو الذاكرة .

هذه الخوارزمية مشابهة لإيجاد ترتيب طوبولوجي.

مثال

ليكن لدينا

رسم بياني تبعية لمثال الخطي C3.
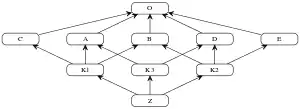
 class O
 class A extends O
 class B extends O
 class C extends O
 class D extends O
 class E extends O
 class K1 extends A, B, C
 class K2 extends D, B, E
 class K3 extends D, A
 class Z extends K1, K2, K3

يتم حساب الخطية لـ Z كـ

  L(O)  := [O]                                                // the linearization of O is trivially the singleton list [O], because O has no parents
 
 L(A)  := [A] + merge(L(O), [O])                             // the linearization of A is A plus the merge of its parents' linearizations with the list of parents...
        = [A] + merge([O], [O])
        = [A, O]                                             // ...which simply prepends A to its single parent's linearization
 
 L(B)  := [B, O]                                             // linearizations of B, C, D and E are computed similar to that of A
 L(C)  := [C, O]
 L(D)  := [D, O]
 L(E)  := [E, O]
 
 L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C])          // first, find the linearizations of K1's parents, L(A), L(B), and L(C), and merge them with the parent list [A, B, C]
        = [K1] + merge([A, O], [B, O], [C, O], [A, B, C])    // class A is a good candidate for the first merge step, because it only appears as the head of the first and last lists
        = [K1, A] + merge([O], [B, O], [C, O], [B, C])       // class O is not a good candidate for the next merge step, because it also appears in the tails of list 2 and 3; but class B is a good candidate
        = [K1, A, B] + merge([O], [O], [C, O], [C])          // class C is a good candidate; class O still appears in the tail of list 3
        = [K1, A, B, C] + merge([O], [O], [O])               // finally, class O is a valid candidate, which also exhausts all remaining lists
        = [K1, A, B, C, O]
 
 L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
        = [K2] + merge([D, O], [B, O], [E, O], [D, B, E])    // select D
        = [K2, D] + merge([O], [B, O], [E, O], [B, E])       // fail O, select B
        = [K2, D, B] + merge([O], [O], [E, O], [E])          // fail O, select E
        = [K2, D, B, E] + merge([O], [O], [O])               // select O
        = [K2, D, B, E, O]
 
 L(K3) := [K3] + merge(L(D), L(A), [D, A])
        = [K3] + merge([D, O], [A, O], [D, A])               // select D
        = [K3, D] + merge([O], [A, O], [A])                  // fail O, select A
        = [K3, D, A] + merge([O], [O])                       // select O
        = [K3, D, A, O]
 
 L(Z)  := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])
        = [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3])    // select K1
        = [Z, K1] + merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3])        // fail A, select K2
        = [Z, K1, K2] + merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3])            // fail A, fail D, select K3
        = [Z, K1, K2, K3] + merge([A, B, C, O], [D, B, E, O], [D, A, O])                  // fail A, select D
        = [Z, K1, K2, K3, D] + merge([A, B, C, O], [B, E, O], [A, O])                     // select A
        = [Z, K1, K2, K3, D, A] + merge([B, C, O], [B, E, O], [O])                        // select B
        = [Z, K1, K2, K3, D, A, B] + merge([C, O], [E, O], [O])                           // select C
        = [Z, K1, K2, K3, D, A, B, C] + merge([O], [E, O], [O])                           // fail O, select E
        = [Z, K1, K2, K3, D, A, B, C, E] + merge([O], [O], [O])                           // select O
        = [Z, K1, K2, K3, D, A, B, C, E, O]                                               // done

المثال موضح في بايثون 3

أولاً، metaclass لتمكين تمثيل قصير للكائنات بالاسم بدلاً من، على سبيل المثال، <class '__main__.A'> <class '__main__.A'> : 

class Type(type):
  def __repr__(cls):
    return cls.__name__ 

class O(object, metaclass=Type): pass

ثم نبني شجرة الميراث. 

class A(O): pass

class B(O): pass

class C(O): pass

class D(O): pass

class E(O): pass

class K1(A, B, C): pass

class K2(D, B, E): pass

class K3(D, A): pass

class Z(K1, K2, K3): pass

و الآن: 

>>> Z.mro()
[Z, K1, K2, K3, D, A, B, C, E, O, <type 'object'>]

المثال موضح في Raku

يستخدم Raku الخطية C3 للفئات افتراضيًا: 

class A {}
class B {}
class C {}
class D {}
class E {}
class K1 is A is B is C {}
class K2 is D is B is E {}
class K3 is D is A {}
class Z is K1 is K2 is K3 {}
say Z.^mro; # OUTPUT: ((Z) (K1) (K2) (K3) (D) (A) (B) (C) (E) (Any) (Mu))

(إن Any و Mu هما الأنواع التي ترثها جميع كائنات Raku)

المراجع
  1. News item on opendylan.org نسخة محفوظة 2020-08-26 على موقع واي باك مشين.
  2. Dylan Enhancement Proposal 3: C3 superclass linearization نسخة محفوظة 2017-07-03 على موقع واي باك مشين.
  3. Python 2.3's use of C3 MRO نسخة محفوظة 2020-08-20 على موقع واي باك مشين.
  4. Tutorial for practical applications of C3 linearization using Python نسخة محفوظة 2020-07-05 على موقع واي باك مشين.
  5. Perl 6's use of the C3 MRO نسخة محفوظة 2016-06-17 على موقع واي باك مشين.
  6. "Parrot uses C3 MRO"، مؤرشف من الأصل في 08 فبراير 2007، اطلع عليه بتاريخ 06 ديسمبر 2006.
  7. Tantau, Till (29 أغسطس 2015)، The TikZ & PGF Manual (PDF) (ط. 3.0.1a)، ص. 956، مؤرشف من الأصل (PDF) في 26 أغسطس 2020، اطلع عليه بتاريخ 14 أغسطس 2017.
  8. C3 MRO available in Perl 5.10 and newer نسخة محفوظة 2013-09-13 على موقع واي باك مشين.
  9. Perl 5 extension for C3 MRO on CPAN نسخة محفوظة 2013-06-06 على موقع واي باك مشين.
  10. van Rossum, Guido (23 يونيو 2010)، "Method Resolution Order"، The History of Python، مؤرشف من الأصل في 08 فبراير 2018، اطلع عليه بتاريخ 18 يناير 2018.
  • بوابة علم الحاسوب
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.