مبرهنة منيلاوس
في الهندسة الرياضية، مبرهنة مينلاوس هي مبرهنة صاغها منيلاوس الإسكندري تتعلق بالمثلثات في المستوي.[1][2][3]

مبرهنة مينلاوس، الحالة الأولى: يمر المستقيم DEF داخل المثلث ABC.
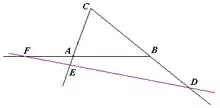
مبرهنة مينلاوس، الحالة الأولى: المستقيم DEF هو بالكامل خارج المثلث ABC.
إذا كانت النقاط الثلاثة A، B، C تشكل مثلثاً هو ABC، وكانت النقاط D، E، F تقع على المستقيمات BC، AC، AB عندها تنص المبرهنة على أن النقاط الثلاثة D, E, F تقع على مستقيم واحد إذا وفقط إذا تحققت العلاقة:
حيث يسمح في هذه النظرية لأطوال الأضلاع بأخذ قيمة سالبة. مثلاً تأخذ النسبة AF / FB قيمة موجبة فقط إذا قطع المستقيم DEF الضلع AB، وبشكل مماثل للكسور الأخرى.
انظر أيضاً
مراجع
- Hopkins, George Irving (1902)، "Art. 983"، Inductive Plane Geometry، D.C. Heath & Co..
- Smith, D.E. (1958)، History of Mathematics، Courier Dover Publications، ج. II، ص. 607، ISBN 0-486-20430-8.
- Rashed, Roshdi (1996)، Encyclopedia of the history of Arabic science، London: Routledge، ج. 2، ص. 483، ISBN 0-415-02063-8.
- بوابة رياضيات
- بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.