متباينة برنولي
في التحليل الحقيقي، متراجحة برنولي المسماة هكذا نسبة إلى ياكوب بيرنولي، هي متراجحة تمكن من الاقتراب من دالة الأس ل.[1]
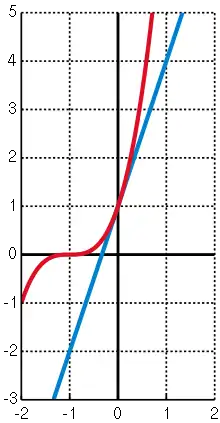
رسم توضيحي لمتباينة برنولي، مع الرسوم البيانية لـ و معروضة باللونين الأحمر والأزرق على التوالي. هنا، .
تنص المتراجحة على أن
لكل عدد صحيح و لكل عدد حقيقي .
برهان المتراجحة
ليكن من . لنبين بالترجع على أن:
الخاصية صحيحة من أجل لأن:
تكافئ .
نفترض أن الخاصية صحيحة من أجل من .إذن:
(لأن )
إذن الخاصية صحيحة من أجل ، و منه النتيجة.
مراجع
- "معلومات عن متباينة برنولي على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 9 نوفمبر 2019.
- Carothers, N.L. (2000)، Real analysis، Cambridge: Cambridge University Press، ص. 9، ISBN 978-0-521-49756-5.
- Bullen, P. S. (2003)، Handbook of means and their inequalities، Dordercht [u.a.]: Kluwer Academic Publ.، ص. 4، ISBN 978-1-4020-1522-9.
- Zaidman, S. (1997)، Advanced calculus : an introduction to mathematical analysis، River Edge, NJ: World Scientific، ص. 32، ISBN 978-981-02-2704-3.
وصلات خارجية
- Bernoulli Inequality by Chris Boucher, Wolfram Demonstrations Project.
- Arthur Lohwater (1982)، "Introduction to Inequalities"، Online e-book in PDF format، مؤرشف من الأصل في 14 أكتوبر 2012.
- Paper “Some Equivalent Forms of Bernoulli’s Inequality: A Survey“
- بوابة تحليل رياضي
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.