نصف قطر الانحناء
في الهندسة الرياضية، نصف قطر الانحناء (R) لمنحنى ما عند نقطة معينة هو قياس نصف قطر القوس الدائري والذي يعتبر أفضل تقريب للمنحنى عند هذه النقطة.[1] حيث أنه معكوس للتقويس (الإنحناء).
- في حالة منحنى فراغى، فإن نصف قطر القوس يساوى طول متجه القوس.
- اما في حالة منحنى مستوى، فإن نصف قطر القوس يساوى القيمة المطلقة ل

حيث s هو طول القوس من نقطة مثبتة على المنحنى، و φ هي الزاوية المماسية و هو الانحناء.
- إذا كان المنحنى المعطى بالإحداثيات الديكارتية (الكارتيزية) مثل (y(x، فإن نصف قطر القوس يكون (بفرض أن المنحنى تفاضلى للدرجة الثانية)
- ، حيث:
، و |z| يعبر عن القيمة المطلقة ل z.
- إذا كان المنحنى المعطى بدلالة الدوال (x(t و (y(t، فإن نصف قطر القوس يكون
- ، حيث:
وبالتجربة، فإنه يمكن تفسير هذه التجربة كالتالي:

الأمثلة
الدوائر وأنصاف الدوائر
- عند وجود نصف دائرة بنصف قطر a في النصف السفلى من المستوى فإن
- عند وجود دائرة نصف قطرها a فإن نصف قطر قوسها يساوى a .
القطع الناقص
- عند وجود قطع ناقص محوره الرئيسى 2a ومحوره الثانوى 2b، فإن قمم (رؤوس) المحور الرئيسى تحتوى على أقل نصف قطر قوس لجميع النقاط
ومن ثم إحتواء قمم (رؤوس) المحور الثانوي على أكبر نصف قطر قوس لجميع النقاط
- .
ملاحظة : عند رسم القوس بحيث يصل بين طرفي المحور الأصغر ومركزه هو طرف المحور الأكبر فمن واقع الرسم يلاحظ أنَّ:-
ناتج المعادلة في حساب نصف قطر الانحناء عند طرف المحور الأكبر أقل من الواقع بمقدار = 0.5 مربع اللا مركزية × نصف المحور الأكبر
إذا رمزنا لنصف القطر بالرمز (نق) فإنَّ:-
طرف المحور الأكبر= 0.5 (1 – (نق الأصغر ÷ نق الأكبر)^2) × نق الأكبر
= 0.5 (نق أكبر – نق الأكبر × (نق الأصغر ÷ نق الأكبر)^2)
= 0.5 (نق أكبر – (نق الأصغر^2 ÷ نق الأكبر))
وبإضافة المقدار الأخير للقانون الأصلي وهو (نق الأصغر^2 ÷ نق الأكبر) تصير العلاقة كما يلي:-
نصف قطر الانحناء = 0.5 نق الأكبر – 0.5 (نق الأصغر^2 ÷ نق الأكبر) + (نق الأصغر^2 ÷ نق الأكبر)
= 0.5 نق الأكبر + 0.5 (نق الأصغر^2 ÷ نق الأكبر)
نصف قطر الانحناء عند المحور الأكبر = 0.5 [ (نق الأصغر^2 ÷ نق الأكبر) + نق الأكبر ]
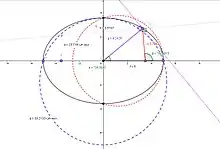
وعند رسم القوس بحيث يصل بين طرفي المحور الأكبر ومركزه هو طرف المحور الأصغر فمن واقع الرسم يلاحظ أنَّ:-
ناتج المعادلة في حساب نصف قطر الانحناء عند القطب أكبر مِن الواقع بمقدار = 0.5 مربع اللا مركزية × مربع نصف المحور الأكبر ÷ نصف المحور الأصغر
= 0.5 (1 – (نق أصغر ÷ نق أكبر)^2) × نق^2 الأكبر ÷ نق الأصغر
= 0.5 [ (نق^2 الأكبر ÷ نق الأصغر) – (نق^2 الأكبر × (نق أصغر ÷ نق أكبر)^2 ÷ نق الأصغر ]
= 0.5 [(نق^2 الأكبر ÷ نق الأصغر) – (نق^2 الأكبر × نق أصغر^2 ÷ (نق أكبر^2 × نق الأصغر) ]
= 0.5 [(نق^2 الأكبر ÷ نق الأصغر) – نق أصغر ]
وبإضافة هذا المقدار للقانون الأصلي
نصف قطر الانحناء عند القطب = (نق أكبر^2 ÷ نق أصغر) - 0.5 [ (نق^2 الأكبر ÷ نق الأصغر) – نق أصغر ]
= (نق أكبر^2 ÷ نق أصغر) - 0.5 (نق^2 الأكبر ÷ نق الأصغر) + 0.5 نق أصغر
= 0.5 (نق^2 الأكبر ÷ نق الأصغر) + 0.5 نق أصغر
نصف قطر الانحناء عند القطب = 0.5 [ (نق^2 الأكبر ÷ نق الأصغر) + نق أصغر ]
حِساب نصف قطر الإنحناء بدلالة الزاوية المركزية
حيث أنَّ قيمة نصف قطر القوس تتغير بتغير طوله فإن معادلات الجيوديسيا تعتمد على المعادلة التالية والتي يكون فيها نصف قطر الانحناء عند الإستواء = نصف القطر الإستوائي وليس قيمة أقل منه،
فبين هذين المحورين a المحور الأكبر أو الرئيس، و b المحور الأصغر أو الثانوي في الـقطع ناقص تكون معادلة حِساب نصف قطر الانحناء كالتالي:[2]
حيث الرمز ثيتا θ يشير إلى رقم دائرة العرض في إحداثيات الكرة الأرضية والذي يُقارب في قيمته قيمة الزاوية المركزية؛
الزاوية المركزية هي الزاوية التي رأسها منتصف المسافة بين بؤرتي القطع الناقص وتحصر هذه الزاوية القوس الواصل بين نُقطة تقاطع المحور الأكبر مع محيط القطع الناقص والنقطة الأخرى التي نحسب نصف قطر الانحناء عندها على سطحه؛
وهي تشبه على سطح الكرة الأرضية الزاوية التي قوسها يمتد بين الاستواء ونقطة شماله أو جنوبه بشرط أن يجمع بينها وبين نظيرتها على الاستواء دائرة عظمى واحدة،
والدوائر العظمى لها أكبر مُحيط على السطح الكروي، وفي حالة كان المحيط يمر بالقطبين فيعتبر المحيط هنا محيطًا بيضاويّ الشكل وهو المقصود تحديدًا لأن بَقيَّة المُحيطات للدوائر العظمى الأخرى تكون قيمها محصورة بين قيمتي المحيط القطبي والمحيط الاستوائي أو تساويه، بمعنى أنَّ النقطتين المعنيتين يقعان على خط طول واحد النقطة على الاستواء والنقطة التي نحسب نصف قطر انحناء القوس عندها، فالزاوية المركزية تحصر القوس الواصل بينهما.
والمقدار هو مقدار مُربع القيمة المحسوبة لجيب هذه الزاوية التي رمزها θ ؛
e معامل التباعد المركزي لـقطع ناقص.
.
وبتطبيق هذا القانون على قطع ناقص محوره الأكبر = نصف القطر الإستوائي للكرة الأرضية فإنه يعطي نصف قطر انحناء قدره = نصف قطر الأرض الإستوائي 6378.137 كم يعني عندما تكون قيمة دائرة العرض = صفرًا
θ=0
وعندما تكون القيمة 90 درجة فإنه يعطي أعلى قيمة لنصف قطر الإنحناء لنقطة على السطح الكروي وهي 6399.594 كم تقريبًا؛
وبقية قيم أنصاف أقطار الانحناء تقع بين هاتين القيمتين حيث تكون قيمة θ تقع في فترة أعداد بين صفر، 90 درجة؛
ملحوظة نصف قطر الانحناء يختلف عن نصف قطر الأرض عند نقطة معينة على دائرة عرض ما وخط طول ما ويمكن أن تُحسَب من العلاقة التالية:-
نصف قطر الأرض عند نقطة تقاطع دائرة عرض وخط طول معلومين = الجذر التربيعي [ س2 + ص2 +ع2 ]
حيث المقدار (س) هو بُعد النقطة عن مستوى الإستواء ويحسب من المعادلة التالية:
س = (نصف قطر الانحناء + الإرتفاع عن سطح البحر) × جيب تمام رقم دائرة العرض × جيب تمام رقم خط الطول
والمقدار (ص) هو بُعد نفس النقطة عن مستوى خط الطول الصفر ويحسب من العلاقة التالية:
ص = (نصف قطر الانحناء + الإرتفاع عن سطح البحر) × جيب تمام رقم دائرة العرض × جيب رقم خط الطول
والمقدار (ع) هو بُعد نفس النقطة عن المستوى الفراغي الثالث العمودي على مستوى الإستواء ومستوى خط الطول الصفر ويحسب من العلاقة التالية:
ع = [ (1 - مربع اللا مركزية للكرة الأرضية) × نصف قطر الانحناء) + الإرتفاع عن سطح البحر ] × جيب رقم دائرة العرض
الزاوية المركزية عند دائرة عرض ما
الزاوية المركزية ليست هي رقم دائرة العرض وإنما مقاربة له ولذلك فالمفترض أن يكون المقدار التالي بصيغة خاصة لكي لا يشتبه الأمر
ومن نفس الإحداثيات الجيوديسية الكارتيزية يمكن حِساب الزاوية المركزية عند دائرة عرض ما وِفق المعادلة التالية:[2]
الزاوية المركزية = قوس ظل [ ع ÷ (س2 + ص2) ]
انظر أيضا
المصادر
- "معلومات عن نصف قطر القوس (رياضيات) على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 11 مايو 2019.
- كتاب أسس المساحة الجيوديسية والجي بي إس لمؤلفه الدكتور جمعة محمد داوود الطبعة الأولى 2012 (PDF)، ص. 20، مؤرشف من الأصل (PDF) في 25 مايو 2020.
2.
- do Carmo, Manfredo [الإنجليزية] (1976). Differential Geometry of Curves and Surfaces. رقم دولي معياري للكتاب 0-13-212589-7.
- بوابة قطارات
- بوابة هندسة رياضية
- بوابة رياضيات
- بوابة الفيزياء
- بوابة نقل
وصلات خارجية
هذا موقع خدمي يتيح التحويل من الإحداثيات الكروية للإحداثيات الكارتيزية بكتابة رقم دائرة العرض وخط الطول والإرتفاع عن سطح البحر فيعطي بالتحويل قيم س X ، ص Y ، ع Z سابقة الذِّكْر.
http://www.apsalin.com/convert-geodetic-to-cartesian.aspx