ω-automaton

Formally, a deterministic ω-automaton is a tuple A = (Q,Σ,δ,Q₀,Acc) that consists of the following components:

• Q is a finite set. The elements of Q are called the states of A.
• Σ is a finite set called the alphabet of A.
• δ: Q × Σ → Q is a function, called the transition function of A.
• Q₀ is an element of Q, called the initial state.
• Acc is the acceptance condition, formally a subset of Q^ω.

An input for A is an infinite string over the alphabet Σ, i.e. it is an infinite sequence α = (a₁,a₂,a₃,...). The run of A on such an input is an infinite sequence ρ = (r₀,r₁,r₂,...) of states, defined as follows:

• r₀ = q₀.
• r₁ = δ(r₀,a₁).
• r₂ = δ(r₁,a₂).

...

• that is, for every i: r_i = δ(r_i-1,a_i).

The main purpose of an ω-automaton is to define a subset of the set of all inputs: The set of accepted inputs. Whereas in the case of an ordinary finite automaton every run ends with a state r_n and the input is accepted if and only if r_n is an accepting state, the definition of the set of accepted inputs is more complicated for ω-automata. Here we must look at the entire run ρ. The input is accepted if the corresponding run is in Acc. The set of accepted input ω-words is called the recognized ω-language by the automaton, which is denoted as L(A).

The definition of Acc as a subset of Q^ω is purely formal and not suitable for practice because normally such sets are infinite. The difference between various types of ω-automata (Büchi, Rabin etc.) consists in how they encode certain subsets Acc of Q^ω as finite sets, and therefore in which such subsets they can encode.

Formally, a nondeterministic ω-automaton is a tuple A = (Q,Σ,Δ,Q₀,Acc) that consists of the following components:

• Q is a finite set. The elements of Q are called the states of A.
• Σ is a finite set called the alphabet of A.
• Δ is a subset of Q × Σ × Q and is called the transition relation of A.
• Q₀ is a subset of Q, called the initial set of states.
• Acc is the acceptance condition, a subset of Q^ω.

Unlike a deterministic ω-automaton, which has a transition function δ, the non-deterministic version has a transition relation Δ. Note that Δ can be regarded as a function : Q × Σ → P(Q) from Q × Σ to the power set P(Q). Thus, given a state q_n and a symbol a_n, the next state q_n+1 is not necessarily determined uniquely, rather there is a set of possible next states.

A run of A on the input α = (a₁,a₂,a₃,...) is any infinite sequence ρ = (r₀,r₁,r₂,...) of states that satisfies the following conditions:

• r₀ is an element of Q₀.
• r₁ is an element of Δ(r₀,a₁).
• r₂ is an element of Δ(r₁,a₂).

...

• that is, for every i: r_i is an element of Δ(r_i-1,a_i).

A nondeterministic ω-automaton may admit many different runs on any given input, or none at all. The input is accepted if at least one of the possible runs is accepting. Whether a run is accepting depends only on Acc, as for deterministic ω-automata. Every deterministic ω-automaton can be regarded as a nondeterministic ω-automaton by taking Δ to be the graph of δ. The definitions of runs and acceptance for deterministic ω-automata are then special cases of the nondeterministic cases.

Acceptance conditions may be infinite sets of ω-words. However, people mostly study acceptance conditions that are finitely representable. The following lists a variety of popular acceptance conditions.

Before discussing the list, let's make the following observation. In the case of infinitely running systems, one is often interested in whether certain behavior is repeated infinitely often. For example, if a network card receives infinitely many ping requests, then it may fail to respond to some of the requests but should respond to an infinite subset of received ping requests. This motivates the following definition: For any run ρ, let Inf(ρ) be the set of states that occur infinitely often in ρ. This notion of certain states being visited infinitely often will be helpful in defining the following acceptance conditions.

• A Büchi automaton is an ω-automaton A that uses the following acceptance condition, for some subset F of Q:

Büchi condition

A accepts exactly those runs ρ for which Inf(ρ) ∩ F is not empty, i.e. there is an accepting state that occurs infinitely often in ρ.

• A Rabin automaton is an ω-automaton A that uses the following acceptance condition, for some set Ω of pairs (B_i,G_i) of sets of states:

Rabin condition

A accepts exactly those runs ρ for which there exists a pair (B_i,G_i) in Ω such that B_i ∩ Inf(ρ) is empty and G_i ∩ Inf(ρ) is not empty.

• A Streett automaton is an ω-automaton A that uses the following acceptance condition, for some set Ω of pairs (B_i,G_i) of sets of states:

Streett condition

A accepts exactly those runs ρ such that for all pairs (B_i,G_i) in Ω, B_i ∩ Inf(ρ) is empty or G_i ∩ Inf(ρ) is not empty.

• A parity automaton is an automaton A whose set of states is Q = {0,1,2,...,k} for some natural number k, and that has the following acceptance condition:

Parity condition

A accepts ρ if and only if the smallest number in Inf(ρ) is even.

• A Muller automaton is an ω-automaton A that uses the following acceptance condition, for a subset F of P(Q) (the power set of Q):

Muller condition

A accepts exactly those runs ρ for which Inf(ρ) is an element of F.

Every Büchi automaton can be regarded as a Muller automaton. It suffices to replace F by F' consisting of all subsets of Q that contain at least one element of F. Similarly every Rabin, Streett or parity automaton can also be regarded as a Muller automaton.

A non-deterministic Büchi automaton that recognizes (0∪1)*0^ω

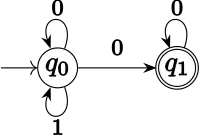
The following ω-language L over the alphabet Σ = {0,1}, which can be recognized by a nondeterministic Büchi automaton: L consists of all ω-words in Σ^ω in which 1 occurs only finitely many times. A non-deterministic Büchi automaton recognizing L needs only two states q₀ (the initial state) and q₁. Δ consists of the triples (q₀,0,q₀), (q₀,1,q₀), (q₀,0,q₁) and (q₁,0,q₁). F = {q₁}. For any input α in which 1 occurs only finitely many times, there is a run that stays in state q₀ as long as there are 1s to read, and goes to state q₁ afterwards. This run is successful. If there are infinitely many 1s, then there is only one possible run: the one that always stays in state q₀. (Once the machine has left q₀ and reached q₁, it cannot return. If another 1 is read, there is no successor state.)

Notice that above language cannot be recognized by a deterministic Büchi automaton, which is strictly less expressive than its non-deterministic counterpart.

An ω-language over a finite alphabet Σ is a set of ω-words over Σ, i.e. it is a subset of Σ^ω. An ω-language over Σ is said to be recognized by an ω-automaton A (with the same alphabet) if it is the set of all ω-words accepted by A. The expressive power of a class of ω-automata is measured by the class of all ω-languages that can be recognized by some automaton in the class.

The nondeterministic Büchi, parity, Rabin, Streett, and Muller automata, respectively, all recognize exactly the same class of ω-languages.[1] These are known as the ω-Kleene closure of the regular languages or as the regular ω-languages. Using different proofs it can also be shown that the deterministic parity, Rabin, Streett, and Muller automata all recognize the regular ω-languages. It follows from this that the class of regular ω-languages is closed under complementation. However, the example above shows that the class of deterministic Büchi automata is strictly weaker.

Because nondeterministic Muller, Rabin, Streett, parity, and Büchi automata are equally expressive, they can be translated to each other. Let us use the following abbreviation ${\displaystyle \{N,D\}\times \{M,R,S,P,B\}}$: for example, NB stands for nondeterministic Büchi ω-automaton, while DP stands for deterministic parity ω-automaton. Then the following holds.

• Clearly, any deterministic automaton can be viewed as a nondeterministic one.
• ${\displaystyle NB\rightarrow NR/NS/NP}$ with no blow-up in the state space.
• ${\displaystyle NR\rightarrow NB}$ with a polynomial blow-up in the state space, i.e., the number of states in the resulting NB is ${\displaystyle 2nm+1}$, where ${\displaystyle n}$ is the number of states in the NB and ${\displaystyle m}$ is the number of Rabin acceptance pairs (see, for example, [2]).
• ${\displaystyle NS/NM/NP\rightarrow NB}$ with exponential blow-up in the state space.
• ${\displaystyle NB\rightarrow DR/DP}$ with exponential blow-up in the state space. This determinization result uses Safra's construction.

A comprehensive overview of translations can be found on the referenced web source. [3]

ω-automata can be used to prove decidability of S1S, the monadic second-order (MSO) theory of natural numbers under successor. Infinite-tree automata extend ω-automata to infinite trees and can be used to prove decidability of S2S, the MSO theory with two successors, and this can be extended to the MSO theory of graphs with bounded (given a fixed bound) treewidth.

• Farwer, Berndt (2002), "ω-Automata", in Grädel, Erich; Thomas, Wolfgang; Wilke, Thomas (eds.), Automata, Logics, and Infinite Games, Lecture Notes in Computer Science, Springer, pp. 3–21, ISBN 978-3-540-00388-5.
• Perrin, Dominique; Pin, Jean-Éric (2004), Infinite Words: Automata, Semigroups, Logic and Games, Elsevier, ISBN 978-0-12-532111-2
• Thomas, Wolfgang (1990), "Automata on infinite objects", in van Leeuwen, Jan (ed.), Handbook of Theoretical Computer Science, vol. B, MIT Press, pp. 133–191, ISBN 978-0-262-22039-2
• Bakhadyr Khoussainov; Anil Nerode (6 December 2012). Automata Theory and its Applications. Springer Science & Business Media. ISBN 978-1-4612-0171-7.