Circular sector
A circular sector, also known as circle sector or disk sector (symbol: ⌔), is the portion of a disk (a closed region bounded by a circle) enclosed by two radii and an arc, with the smaller area being known as the minor sector and the larger being the major sector.[1] In the diagram, θ is the central angle, the radius of the circle, and is the arc length of the minor sector.
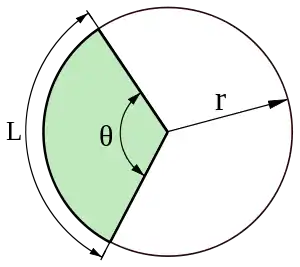
The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle.[2]
Types
A sector with the central angle of 180° is called a half-disk and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, such as quadrants (90°), sextants (60°), and octants (45°), which come from the sector being one 4th, 6th or 8th part of a full circle, respectively. Confusingly, the arc of a quadrant (a circular arc) can also be termed a quadrant.
Compass

Traditionally wind directions on the compass rose are given as one of the 8 octants (N, NE, E, SE, S, SW, W, NW) because that is more precise than merely giving one of the 4 quadrants, and the wind vane typically does not have enough accuracy to allow more precise indication.
The name of the instrument "octant" comes from the fact that it is based on 1/8th of the circle. Most commonly, octants are seen on the compass rose.
Area
The total area of a circle is πr2. The area of the sector can be obtained by multiplying the circle's area by the ratio of the angle θ (expressed in radians) and 2π (because the area of the sector is directly proportional to its angle, and 2π is the angle for the whole circle, in radians):
The area of a sector in terms of L can be obtained by multiplying the total area πr2 by the ratio of L to the total perimeter 2πr.
Another approach is to consider this area as the result of the following integral:
Converting the central angle into degrees gives[3]
Perimeter
The length of the perimeter of a sector is the sum of the arc length and the two radii:
where θ is in radians.
Arc length
The formula for the length of an arc is:[4]
where L represents the arc length, r represents the radius of the circle and θ represents the angle in radians made by the arc at the centre of the circle.[5]
If the value of angle is given in degrees, then we can also use the following formula by:[3]
Chord length
The length of a chord formed with the extremal points of the arc is given by
where C represents the chord length, R represents the radius of the circle, and θ represents the angular width of the sector in radians.
See also
- Circular segment – the part of the sector which remains after removing the triangle formed by the center of the circle and the two endpoints of the circular arc on the boundary.
- Conic section
- Earth quadrant
- Sector of (mathematics)
- Spherical sector – the analogous 3D figure
References
- Dewan, Rajesh K. (2016). Saraswati Mathematics. New Delhi: New Saraswati House India Pvt Ltd. p. 234. ISBN 978-8173358371.
- Achatz, Thomas; Anderson, John G. (2005). Technical shop mathematics. Kathleen McKenzie (3rd ed.). New York: Industrial Press. p. 376. ISBN 978-0831130862. OCLC 56559272.
- Uppal, Shveta (2019). Mathematics: Textbook for class X. New Delhi: National Council of Educational Research and Training. pp. 226, 227. ISBN 978-81-7450-634-4. OCLC 1145113954.
- Larson, Ron; Edwards, Bruce H. (2002). Calculus I with Precalculus (3rd ed.). Boston, MA.: Brooks/Cole. p. 570. ISBN 978-0-8400-6833-0. OCLC 706621772.
- Wicks, Alan (2004). Mathematics Standard Level for the International Baccalaureate : a text for the new syllabus. West Conshohocken, PA: Infinity Publishing.com. p. 79. ISBN 0-7414-2141-0. OCLC 58869667.
Sources
- Gerard, L. J. V., The Elements of Geometry, in Eight Books; or, First Step in Applied Logic (London, Longmans, Green, Reader and Dyer, 1874), p. 285.
- Legendre, A. M., Elements of Geometry and Trigonometry, Charles Davies, ed. (New York: A. S. Barnes & Co., 1858), p. 119.