Torus knot

A torus knot can be rendered geometrically in multiple ways which are topologically equivalent (see Properties below) but geometrically distinct. The convention used in this article and its figures is the following.

The (p,q)-torus knot winds q times around a circle in the interior of the torus, and p times around its axis of rotational symmetry.[note 1]. If p and q are not relatively prime, then we have a torus link with more than one component.

The direction in which the strands of the knot wrap around the torus is also subject to differing conventions. The most common is to have the strands form a right-handed screw for p q > 0.[3][4][5]

The (p,q)-torus knot can be given by the parametrization

${\displaystyle {\begin{aligned}x&=r\cos(p\phi )\\y&=r\sin(p\phi )\\z&=-\sin(q\phi )\end{aligned}}}$

where ${\displaystyle r=\cos(q\phi )+2}$ and ${\displaystyle 0<\phi <2\pi }$. This lies on the surface of the torus given by ${\displaystyle (r-2)^{2}+z^{2}=1}$ (in cylindrical coordinates).

Other parameterizations are also possible, because knots are defined up to continuous deformation. The illustrations for the (2,3)- and (3,8)-torus knots can be obtained by taking ${\displaystyle r=\cos(q\phi )+4}$, and in the case of the (2,3)-torus knot by furthermore subtracting respectively ${\displaystyle 3\cos((p-q)\phi )}$ and ${\displaystyle 3\sin((p-q)\phi )}$ from the above parameterizations of x and y. The latter generalizes smoothly to any coprime p,q satisfying ${\displaystyle p<q<2p}$.

Diagram of a (3,−8)-torus knot.

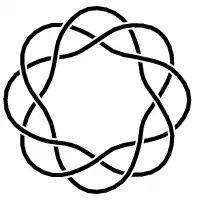
A torus knot is trivial iff either p or q is equal to 1 or −1.[4][5]

Each nontrivial torus knot is prime[6] and chiral.[4]

The (p,q) torus knot is equivalent to the (q,p) torus knot.[3][5] This can be proved by moving the strands on the surface of the torus.[7] The (p,−q) torus knot is the obverse (mirror image) of the (p,q) torus knot.[5] The (−p,−q) torus knot is equivalent to the (p,q) torus knot except for the reversed orientation.

The (3, 4) torus knot on the unwrapped torus surface, and its braid word

Any (p,q)-torus knot can be made from a closed braid with p strands. The appropriate braid word is [8]

${\displaystyle (\sigma _{1}\sigma _{2}\cdots \sigma _{p-1})^{q}.}$

(This formula assumes the common convention that braid generators are right twists,[4][8][9][10] which is not followed by the Wikipedia page on braids.)

The crossing number of a (p,q) torus knot with p,q > 0 is given by

c = min((p−1)q, (q−1)p).

The genus of a torus knot with p,q > 0 is

${\displaystyle g={\frac {1}{2}}(p-1)(q-1).}$

The Alexander polynomial of a torus knot is [3][8]

${\displaystyle t^{k}{\frac {(t^{pq}-1)(t-1)}{(t^{p}-1)(t^{q}-1)}},}$ where ${\displaystyle k=-{\frac {(p-1)(q-1)}{2}}.}$

The Jones polynomial of a (right-handed) torus knot is given by

${\displaystyle t^{(p-1)(q-1)/2}{\frac {1-t^{p+1}-t^{q+1}+t^{p+q}}{1-t^{2}}}.}$

The complement of a torus knot in the 3-sphere is a Seifert-fibered manifold, fibred over the disc with two singular fibres.

Let Y be the p-fold dunce cap with a disk removed from the interior, Z be the q-fold dunce cap with a disk removed from its interior, and X be the quotient space obtained by identifying Y and Z along their boundary circle. The knot complement of the (p, q) -torus knot deformation retracts to the space X. Therefore, the knot group of a torus knot has the presentation

${\displaystyle \langle x,y\mid x^{p}=y^{q}\rangle .}$

Torus knots are the only knots whose knot groups have nontrivial center (which is infinite cyclic, generated by the element ${\displaystyle x^{p}=y^{q}}$ in the presentation above).

The stretch factor of the (p,q) torus knot, as a curve in Euclidean space, is Ω(min(p,q)), so torus knots have unbounded stretch factors. Undergraduate researcher John Pardon won the 2012 Morgan Prize for his research proving this result, which solved a problem originally posed by Mikhail Gromov.[11][12]

The (p,q)−torus knots arise when considering the link of an isolated complex hypersurface singularity. One intersects the complex hypersurface with a hypersphere, centred at the isolated singular point, and with sufficiently small radius so that it does not enclose, nor encounter, any other singular points. The intersection gives a submanifold of the hypersphere.

Let p and q be coprime integers, greater than or equal to two. Consider the holomorphic function ${\displaystyle f:\mathbb {C} ^{2}\to \mathbb {C} }$ given by ${\displaystyle f(w,z):=w^{p}+z^{q}.}$ Let ${\displaystyle V_{f}\subset \mathbb {C} ^{2}}$ be the set of ${\displaystyle (w,z)\in \mathbb {C} ^{2}}$ such that ${\displaystyle f(w,z)=0.}$ Given a real number ${\displaystyle 0<\varepsilon \ll 1,}$ we define the real three-sphere ${\displaystyle \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {R} ^{4}\hookrightarrow \mathbb {C} ^{2}}$ as given by ${\displaystyle |w|^{2}+|z|^{2}=\varepsilon ^{2}.}$ The function ${\displaystyle f}$ has an isolated critical point at ${\displaystyle (0,0)\in \mathbb {C} ^{2}}$ since ${\displaystyle \partial f/\partial w=\partial f/\partial z=0}$ if and only if ${\displaystyle w=z=0.}$ Thus, we consider the structure of ${\displaystyle V_{f}}$ close to ${\displaystyle (0,0)\in \mathbb {C} ^{2}.}$ In order to do this, we consider the intersection ${\displaystyle V_{f}\cap \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {S} _{\varepsilon }^{3}.}$ This intersection is the so-called link of the singularity ${\displaystyle f(w,z)=w^{p}+z^{q}.}$ The link of ${\displaystyle f(w,z)=w^{p}+z^{q}}$, where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.[13]

(36,3) torus link

The figure on the right is torus link (72,4) .

• Unknot, 3₁ knot (3,2), 5₁ knot (5,2), 7₁ knot (7,2), 8₁₉ knot (4,3), 9₁ knot (9,2), 10₁₂₄ knot (5,3)

Table #	A-B	Image	P	Q	Cross #
0	01				0
3a1	31		2	3	3
5a2	51		2	5	5
7a7	71		2	7	7
8n3	819		3	4	8
9a41	91		2	9	9
10n21	10124		3	5	10
11a367			2	11	11
13a4878			2	13	13
14n21881			3	7	14
15n41185			4	5	15
15a85263			2	15	15
16n783154			3	8	16
			2	17	17
			2	19	19
			3	10	20
			4	7	21
			2	21	21
			3	11	22
			2	23	23
			5	6	24
			2	25	25
			3	13	26
			4	9	27
			2	27	27
			5	7	28
			3	14	28
			2	29	29
			2	31	31
			5	8	32
			3	16	32
			4	11	33
			2	33	33
			3	17	34
			6	7	35
			2	35	35
			5	9	36
			7	8	48
			7	9	54
			8	9	63

A g-torus knot is a closed curve drawn on a g-torus. More technically, it is the homeomorphic image of a circle in S³ which can be realized as a subset of a genus g handlebody in S³ (whose complement is also a genus g handlebody). If a link is a subset of a genus two handlebody, it is a double torus link.[14]

For genus two, the simplest example of a double torus knot that is not a torus knot is the figure-eight knot.[15][16]

• Alternating knot
• Satellite knot
• Hyperbolic knot
• Irrational winding of a torus
• Topopolis

• "36 Torus Knots", The Knot Atlas.
• Weisstein, Eric W. "Torus Knot". MathWorld.
• Torus knot renderer in Actionscript
• Fun with the PQ-Torus Knot