Alternated hexagonal tiling honeycomb

In three-dimensional hyperbolic geometry, the alternated hexagonal tiling honeycomb, h{6,3,3}, or , is a semiregular tessellation with tetrahedron and triangular tiling cells arranged in an octahedron vertex figure. It is named after its construction, as an alteration of a hexagonal tiling honeycomb.

Alternated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbols	h{6,3,3} s{3,6,3} 2s{6,3,6} 2s{6,3^[3]} s{3^[3,3]}
Coxeter diagrams	↔ ↔ ↔ ↔
Cells	{3,3} {3^[3]}
Faces	triangle {3}
Vertex figure	truncated tetrahedron
Coxeter groups	${\overline {P}}_{3}$ , [3,3^[3]] 1/2 ${\overline {V}}_{3}$ , [6,3,3] 1/2 ${\overline {Y}}_{3}$ , [3,6,3] 1/2 ${\overline {Z}}_{3}$ , [6,3,6] 1/2 ${\overline {VP}}_{3}$ , [6,3^[3]] 1/2 ${\overline {PP}}_{3}$ , [3^[3,3]]
Properties	Vertex-transitive, edge-transitive, quasiregular

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Symmetry constructions

Subgroup relations

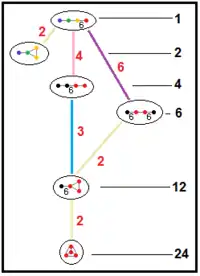
It has five alternated constructions from reflectional Coxeter groups all with four mirrors and only the first being regular: [6,3,3], [3,6,3], [6,3,6], [6,3^[3]] and [3^[3,3]] , having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)^*] (remove 3 mirrors, index 24 subgroup); [3,6,3^*] or [3^*,6,3] (remove 2 mirrors, index 6 subgroup); [1⁺,6,3,6,1⁺] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3^[3,3]]. The ringed Coxeter diagrams are , , , and , representing different types (colors) of hexagonal tilings in the Wythoff construction.

Related honeycombs

The alternated hexagonal tiling honeycomb has 3 related forms: the cantic hexagonal tiling honeycomb, ; the runcic hexagonal tiling honeycomb, ; and the runcicantic hexagonal tiling honeycomb, .

Cantic hexagonal tiling honeycomb

Cantic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h₂{6,3,3}
Coxeter diagrams	↔
Cells	r{3,3} t{3,3} h₂{6,3}
Faces	triangle {3} hexagon {6}
Vertex figure	wedge
Coxeter groups	${\overline {P}}_{3}$ , [3,3^[3]]
Properties	Vertex-transitive

The cantic hexagonal tiling honeycomb, h₂{6,3,3}, or , is composed of octahedron, truncated tetrahedron, and trihexagonal tiling facets, with a wedge vertex figure.

Runcic hexagonal tiling honeycomb

Runcic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h₃{6,3,3}
Coxeter diagrams	↔
Cells	{3,3} {}x{3} rr{3,3} {3^[3]}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	triangular cupola
Coxeter groups	${\overline {P}}_{3}$ , [3,3^[3]]
Properties	Vertex-transitive

The runcic hexagonal tiling honeycomb, h₃{6,3,3}, or , has tetrahedron, triangular prism, cuboctahedron, and triangular tiling facets, with a triangular cupola vertex figure.

Runcicantic hexagonal tiling honeycomb

Runcicantic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h_2,3{6,3,3}
Coxeter diagrams	↔
Cells	t{3,3} {}x{3} tr{3,3} h₂{6,3}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	rectangular pyramid
Coxeter groups	${\overline {P}}_{3}$ , [3,3^[3]]
Properties	Vertex-transitive

The runcicantic hexagonal tiling honeycomb, h_2,3{6,3,3}, or , has truncated tetrahedron, triangular prism, truncated octahedron, and trihexagonal tiling facets, with a rectangular pyramid vertex figure.

References

Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space Archived 2016-06-10 at the Wayback Machine) Table III
Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353
N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H³: p130.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.