Analog computer

An analog computer or analogue computer is a type of computer that uses the continuous variation aspect of physical phenomena such as electrical, mechanical, or hydraulic quantities (analog signals) to model the problem being solved. In contrast, digital computers represent varying quantities symbolically and by discrete values of both time and amplitude (digital signals).

For the Atari 8-bit computer magazine, see ANALOG Computing.

A page from the Bombardier's Information File (BIF) that describes the components and controls of the Norden bombsight. It was a highly sophisticated optical/mechanical analog computer used by the United States Army Air Force during World War II, the Korean War, and the Vietnam War to aid the pilot of a bomber aircraft in dropping bombs accurately.
TR-10 desktop analog computer of the late 1960s and early 1970s

Analog computers can have a very wide range of complexity. Slide rules and nomograms are the simplest, while naval gunfire control computers and large hybrid digital/analog computers were among the most complicated.[1] Complex mechanisms for process control and protective relays used analog computation to perform control and protective functions.

Analog computers were widely used in scientific and industrial applications even after the advent of digital computers, because at the time they were typically much faster, but they started to become obsolete as early as the 1950s and 1960s, although they remained in use in some specific applications, such as aircraft flight simulators, the flight computer in aircraft, and for teaching control systems in universities. Perhaps the most relatable example of analog computers are mechanical watches where the continuous and periodic rotation of interlinked gears drives the second, minute and hour needles in the clock. More complex applications, such as aircraft flight simulators and synthetic-aperture radar, remained the domain of analog computing (and hybrid computing) well into the 1980s, since digital computers were insufficient for the task.[2]

Timeline of analog computers
See also: History of computing hardware § Analog computers

Precursors
See also: Timeline of computing hardware before 1950

This is a list of examples of early computation devices considered precursors of the modern computers. Some of them may even have been dubbed 'computers' by the press, though they may fail to fit modern definitions.

The Antikythera mechanism, dating between 150 and 100 BC, was an early analog computer.

The Antikythera mechanism, a type of device used to determine the positions of heavenly bodies known as an orrery, was described as an early mechanical analog computer by British physicist, information scientist, and historian of science Derek J. de Solla Price.[3] It was discovered in 1901, in the Antikythera wreck off the Greek island of Antikythera, between Kythera and Crete, and has been dated to c. 150~100 BC, during the Hellenistic period. Devices of a level of complexity comparable to that of the Antikythera mechanism would not reappear until a thousand years later.

Many mechanical aids to calculation and measurement were constructed for astronomical and navigation use. The planisphere was first described by Ptolemy in the 2nd century AD. The astrolabe was invented in the Hellenistic world in either the 1st or 2nd centuries BC and is often attributed to Hipparchus. A combination of the planisphere and dioptra, the astrolabe was effectively an analog computer capable of working out several different kinds of problems in spherical astronomy. An astrolabe incorporating a mechanical calendar computer[4][5] and gear-wheels was invented by Abi Bakr of Isfahan, Persia in 1235.[6] Abū Rayhān al-Bīrūnī invented the first mechanical geared lunisolar calendar astrolabe,[7] an early fixed-wired knowledge processing machine[8] with a gear train and gear-wheels,[9] c. AD 1000.

The sector, a calculating instrument used for solving problems in proportion, trigonometry, multiplication and division, and for various functions, such as squares and cube roots, was developed in the late 16th century and found application in gunnery, surveying and navigation.

The planimeter was a manual instrument to calculate the area of a closed figure by tracing over it with a mechanical linkage.

A slide rule. The sliding central slip is set to 1.3, the cursor to 2.0 and points to the multiplied result of 2.6.

The slide rule was invented around 1620–1630, shortly after the publication of the concept of the logarithm. It is a hand-operated analog computer for doing multiplication and division. As slide rule development progressed, added scales provided reciprocals, squares and square roots, cubes and cube roots, as well as transcendental functions such as logarithms and exponentials, circular and hyperbolic trigonometry and other functions. Aviation is one of the few fields where slide rules are still in widespread use, particularly for solving time–distance problems in light aircraft.

In 1831–1835, mathematician and engineer Giovanni Plana devised a perpetual-calendar machine, which, through a system of pulleys and cylinders, could predict the perpetual calendar for every year from AD 0 (that is, 1 BC) to AD 4000, keeping track of leap years and varying day length.[10]

The tide-predicting machine invented by Sir William Thomson in 1872 was of great utility to navigation in shallow waters. It used a system of pulleys and wires to automatically calculate predicted tide levels for a set period at a particular location.

The differential analyser, a mechanical analog computer designed to solve differential equations by integration, used wheel-and-disc mechanisms to perform the integration. In 1876 James Thomson had already discussed the possible construction of such calculators, but he had been stymied by the limited output torque of the ball-and-disk integrators. A number of similar systems followed, notably those of the Spanish engineer Leonardo Torres Quevedo, who built several machines for solving real and complex roots of polynomials;[11][12][13] and Michelson and Stratton, whose Harmonic Analyser performed Fourier analysis, but using an array of 80 springs rather than Kelvin integrators. This work led to the mathematical understanding of the Gibbs phenomenon of overshoot in Fourier representation near discontinuities.[14] In a differential analyzer, the output of one integrator drove the input of the next integrator, or a graphing output. The torque amplifier was the advance that allowed these machines to work. Starting in the 1920s, Vannevar Bush and others developed mechanical differential analyzers.

Modern era
Analog computing machine at the Lewis Flight Propulsion Laboratory c. 1949.
Heathkit EC-1 educational analog computer

The Dumaresq was a mechanical calculating device invented around 1902 by Lieutenant John Dumaresq of the Royal Navy. It was an analog computer that related vital variables of the fire control problem to the movement of one's own ship and that of a target ship. It was often used with other devices, such as a Vickers range clock to generate range and deflection data so the gun sights of the ship could be continuously set. A number of versions of the Dumaresq were produced of increasing complexity as development proceeded.

By 1912, Arthur Pollen had developed an electrically driven mechanical analog computer for fire-control systems, based on the differential analyser. It was used by the Imperial Russian Navy in World War I.[15]

Starting in 1929, AC network analyzers were constructed to solve calculation problems related to electrical power systems that were too large to solve with numerical methods at the time.[16] These were essentially scale models of the electrical properties of the full-size system. Since network analyzers could handle problems too large for analytic methods or hand computation, they were also used to solve problems in nuclear physics and in the design of structures. More than 50 large network analyzers were built by the end of the 1950s.

World War II era gun directors, gun data computers, and bomb sights used mechanical analog computers. In 1942 Helmut Hölzer built a fully electronic analog computer at Peenemünde Army Research Center[17][18][19] as an embedded control system (mixing device) to calculate V-2 rocket trajectories from the accelerations and orientations (measured by gyroscopes) and to stabilize and guide the missile.[20][21] Mechanical analog computers were very important in gun fire control in World War II, the Korean War and well past the Vietnam War; they were made in significant numbers.

In the period 1930–1945 in the Netherlands, Johan van Veen developed an analogue computer to calculate and predict tidal currents when the geometry of the channels are changed. Around 1950, this idea was developed into the Deltar, a hydraulic analogy computer supporting the closure of estuaries in the southwest of the Netherlands (the Delta Works).

The FERMIAC was an analog computer invented by physicist Enrico Fermi in 1947 to aid in his studies of neutron transport.[22] Project Cyclone was an analog computer developed by Reeves in 1950 for the analysis and design of dynamic systems.[23] Project Typhoon was an analog computer developed by RCA in 1952. It consisted of over 4,000 electron tubes and used 100 dials and 6,000 plug-in connectors to program.[24] The MONIAC Computer was a hydraulic analogy of a national economy first unveiled in 1949.[25]

Computer Engineering Associates was spun out of Caltech in 1950 to provide commercial services using the "Direct Analogy Electric Analog Computer" ("the largest and most impressive general-purpose analyzer facility for the solution of field problems") developed there by Gilbert D. McCann, Charles H. Wilts, and Bart Locanthi.[26][27]

Educational analog computers illustrated the principles of analog calculation. The Heathkit EC-1, a $199 educational analog computer, was made by the Heath Company, US c. 1960.[28] It was programmed using patch cords that connected nine operational amplifiers and other components.[29] General Electric also marketed an "educational" analog computer kit of a simple design in the early 1960s consisting of two transistor tone generators and three potentiometers wired such that the frequency of the oscillator was nulled when the potentiometer dials were positioned by hand to satisfy an equation. The relative resistance of the potentiometer was then equivalent to the formula of the equation being solved. Multiplication or division could be performed, depending on which dials were inputs and which was the output. Accuracy and resolution was limited and a simple slide rule was more accurate. However, the unit did demonstrate the basic principle.

Analog computer designs were published in electronics magazines. One example is the PEAC (Practical Electronics analogue computer), published in Practical Electronics in the January 1968 edition.[30] Another more modern hybrid computer design was published in Everyday Practical Electronics in 2002.[31] An example described in the EPE hybrid computer was the flight of a VTOL aircraft such as the Harrier jump jet.[31] The altitude and speed of the aircraft were calculated by the analog part of the computer and sent to a PC via a digital microprocessor and displayed on the PC screen.

In industrial process control, analog loop controllers were used to automatically regulate temperature, flow, pressure, or other process conditions. The technology of these controllers ranged from purely mechanical integrators, through vacuum-tube and solid-state devices, to emulation of analog controllers by microprocessors.

Electronic analog computers
Polish analog computer AKAT-1 (1959)
EAI 8800 Analog computing system used for hardware-in-the-loop simulation of a Claas tractor (1986)

The similarity between linear mechanical components, such as springs and dashpots (viscous-fluid dampers), and electrical components, such as capacitors, inductors, and resistors is striking in terms of mathematics. They can be modeled using equations of the same form.

However, the difference between these systems is what makes analog computing useful. Complex systems often are not amenable to pen-and-paper analysis, and require some form of testing or simulation. Complex mechanical systems, such as suspensions for racing cars, are expensive to fabricate and hard to modify. And taking precise mechanical measurements during high-speed tests adds further difficulty.

By contrast, it is very inexpensive to build an electrical equivalent of a complex mechanical system, to simulate its behavior. Engineers arrange a few operational amplifiers (op amps) and some passive linear components to form a circuit that follows the same equations as the mechanical system being simulated. All measurements can be taken directly with an oscilloscope. In the circuit, the (simulated) stiffness of the spring, for instance, can be changed by adjusting the parameters of an integrator. The electrical system is an analogy to the physical system, hence the name, but it is much less expensive than a mechanical prototype, much easier to modify, and generally safer.

The electronic circuit can also be made to run faster or slower than the physical system being simulated. Experienced users of electronic analog computers said that they offered a comparatively intimate control and understanding of the problem, relative to digital simulations.

OME P2, 1952, a French electronic analog computer from Société d'Electronique et d'Automatisme (SEA)

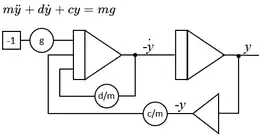
Electronic analog computers are especially well-suited to representing situations described by differential equations. Historically, they were often used when a system of differential equations proved very difficult to solve by traditional means. As a simple example, the dynamics of a spring-mass system can be described by the equation , with as the vertical position of a mass , the damping coefficient, the spring constant and the gravity of Earth. For analog computing, the equation is programmed as . The equivalent analog circuit consists of two integrators for the state variables (speed) and (position), one inverter, and three potentiometers.

Electronic analog computers have drawbacks: the value of the circuit's supply voltage limits the range over which the variables may vary (since the value of a variable is represented by a voltage on a particular wire). Therefore, each problem must be scaled so its parameters and dimensions can be represented using voltages that the circuit can supply —e.g., the expected magnitudes of the velocity and the position of a spring pendulum. Improperly scaled variables can have their values "clamped" by the limits of the supply voltage. Or if scaled too small, they can suffer from higher noise levels. Either problem can cause the circuit to produce an incorrect simulation of the physical system. (Modern digital simulations are much more robust to widely varying values of their variables, but are still not entirely immune to these concerns: floating-point digital calculations support a huge dynamic range, but can suffer from imprecision if tiny differences of huge values lead to numerical instability.)

Analog circuit for the dynamics of a spring-mass system (without scaling factors)
Damped motion of a spring-mass system

The precision of the analog computer readout was limited chiefly by the precision of the readout equipment used, generally three or four significant figures. (Modern digital simulations are much better in this area. Digital arbitrary-precision arithmetic can provide any desired degree of precision.) However, in most cases the precision of an analog computer is absolutely sufficient given the uncertainty of the model characteristics and its technical parameters.

Many small computers dedicated to specific computations are still part of industrial regulation equipment, but from the 1950s to the 1970s, general-purpose analog computers were the only systems fast enough for real time simulation of dynamic systems, especially in the aircraft, military and aerospace field.

In the 1960s, the major manufacturer was Electronic Associates of Princeton, New Jersey, with its 231R Analog Computer (vacuum tubes, 20 integrators) and subsequently its EAI 8800 Analog Computer (solid state operational amplifiers, 64 integrators).[32] Its challenger was Applied Dynamics of Ann Arbor, Michigan.

Although the basic technology for analog computers is usually operational amplifiers (also called "continuous current amplifiers" because they have no low frequency limitation), in the 1960s an attempt was made in the French ANALAC computer to use an alternative technology: medium frequency carrier and non dissipative reversible circuits.

In the 1970s, every large company and administration concerned with problems in dynamics had an analog computing center, such as:

Analog–digital hybrids

Analog computing devices are fast; digital computing devices are more versatile and accurate. The idea behind an analog-digital hybrid is to combine the two processes for the best efficiency. An example of such hybrid elementary device is the hybrid multiplier, where one input is an analog signal, the other input is a digital signal and the output is analog. It acts as an analog potentiometer, upgradable digitally. This kind of hybrid technique is mainly used for fast dedicated real time computation when computing time is very critical, as signal processing for radars and generally for controllers in embedded systems.

In the early 1970s, analog computer manufacturers tried to tie together their analog computers with a digital computers to get the advantages of the two techniques. In such systems, the digital computer controlled the analog computer, providing initial set-up, initiating multiple analog runs, and automatically feeding and collecting data. The digital computer may also participate to the calculation itself using analog-to-digital and digital-to-analog converters.

The largest manufacturer of hybrid computers was Electronic Associates. Their hybrid computer model 8900 was made of a digital computer and one or more analog consoles. These systems were mainly dedicated to large projects such as the Apollo program and Space Shuttle at NASA, or Ariane in Europe, especially during the integration step where at the beginning everything is simulated, and progressively real components replace their simulated parts.[33]

Only one company was known as offering general commercial computing services on its hybrid computers, CISI of France, in the 1970s.

The best reference in this field is the 100,000 simulation runs for each certification of the automatic landing systems of Airbus and Concorde aircraft.[34]

After 1980, purely digital computers progressed more and more rapidly and were fast enough to compete with analog computers. One key to the speed of analog computers was their fully parallel computation, but this was also a limitation. The more equations required for a problem, the more analog components were needed, even when the problem wasn't time critical. "Programming" a problem meant interconnecting the analog operators; even with a removable wiring panel this was not very versatile. Today there are no more big hybrid computers, but only hybrid components.

Implementations

Mechanical analog computers
Main article: Mechanical computer
William Ferrel's tide-predicting machine of 1881–1882

While a wide variety of mechanisms have been developed throughout history, some stand out because of their theoretical importance, or because they were manufactured in significant quantities.

Most practical mechanical analog computers of any significant complexity used rotating shafts to carry variables from one mechanism to another. Cables and pulleys were used in a Fourier synthesizer, a tide-predicting machine, which summed the individual harmonic components. Another category, not nearly as well known, used rotating shafts only for input and output, with precision racks and pinions. The racks were connected to linkages that performed the computation. At least one U.S. Naval sonar fire control computer of the later 1950s, made by Librascope, was of this type, as was the principal computer in the Mk. 56 Gun Fire Control System.

Online, there is a remarkably clear illustrated reference (OP 1140)[35] that describes the fire control computer mechanisms.[35] For adding and subtracting, precision miter-gear differentials were in common use in some computers; the Ford Instrument Mark I Fire Control Computer contained about 160 of them.

Integration with respect to another variable was done by a rotating disc driven by one variable. Output came from a pick-off device (such as a wheel) positioned at a radius on the disc proportional to the second variable. (A carrier with a pair of steel balls supported by small rollers worked especially well. A roller, its axis parallel to the disc's surface, provided the output. It was held against the pair of balls by a spring.)

Arbitrary functions of one variable were provided by cams, with gearing to convert follower movement to shaft rotation.

Functions of two variables were provided by three-dimensional cams. In one good design, one of the variables rotated the cam. A hemispherical follower moved its carrier on a pivot axis parallel to that of the cam's rotating axis. Pivoting motion was the output. The second variable moved the follower along the axis of the cam. One practical application was ballistics in gunnery.

Coordinate conversion from polar to rectangular was done by a mechanical resolver (called a "component solver" in US Navy fire control computers). Two discs on a common axis positioned a sliding block with pin (stubby shaft) on it. One disc was a face cam, and a follower on the block in the face cam's groove set the radius. The other disc, closer to the pin, contained a straight slot in which the block moved. The input angle rotated the latter disc (the face cam disc, for an unchanging radius, rotated with the other (angle) disc; a differential and a few gears did this correction).

Referring to the mechanism's frame, the location of the pin corresponded to the tip of the vector represented by the angle and magnitude inputs. Mounted on that pin was a square block.

Rectilinear-coordinate outputs (both sine and cosine, typically) came from two slotted plates, each slot fitting on the block just mentioned. The plates moved in straight lines, the movement of one plate at right angles to that of the other. The slots were at right angles to the direction of movement. Each plate, by itself, was like a Scotch yoke, known to steam engine enthusiasts.

During World War II, a similar mechanism converted rectilinear to polar coordinates, but it was not particularly successful and was eliminated in a significant redesign (USN, Mk. 1 to Mk. 1A).

Multiplication was done by mechanisms based on the geometry of similar right triangles. Using the trigonometric terms for a right triangle, specifically opposite, adjacent, and hypotenuse, the adjacent side was fixed by construction. One variable changed the magnitude of the opposite side. In many cases, this variable changed sign; the hypotenuse could coincide with the adjacent side (a zero input), or move beyond the adjacent side, representing a sign change.

Typically, a pinion-operated rack moving parallel to the (trig.-defined) opposite side would position a slide with a slot coincident with the hypotenuse. A pivot on the rack let the slide's angle change freely. At the other end of the slide (the angle, in trig. terms), a block on a pin fixed to the frame defined the vertex between the hypotenuse and the adjacent side.

At any distance along the adjacent side, a line perpendicular to it intersects the hypotenuse at a particular point. The distance between that point and the adjacent side is some fraction that is the product of 1 the distance from the vertex, and 2 the magnitude of the opposite side.

The second input variable in this type of multiplier positions a slotted plate perpendicular to the adjacent side. That slot contains a block, and that block's position in its slot is determined by another block right next to it. The latter slides along the hypotenuse, so the two blocks are positioned at a distance from the (trig.) adjacent side by an amount proportional to the product.

To provide the product as an output, a third element, another slotted plate, also moves parallel to the (trig.) opposite side of the theoretical triangle. As usual, the slot is perpendicular to the direction of movement. A block in its slot, pivoted to the hypotenuse block positions it.

A special type of integrator, used at a point where only moderate accuracy was needed, was based on a steel ball, instead of a disc. It had two inputs, one to rotate the ball, and the other to define the angle of the ball's rotating axis. That axis was always in a plane that contained the axes of two movement pick-off rollers, quite similar to the mechanism of a rolling-ball computer mouse (in that mechanism, the pick-off rollers were roughly the same diameter as the ball). The pick-off roller axes were at right angles.

A pair of rollers "above" and "below" the pick-off plane were mounted in rotating holders that were geared together. That gearing was driven by the angle input, and established the rotating axis of the ball. The other input rotated the "bottom" roller to make the ball rotate.

Essentially, the whole mechanism, called a component integrator, was a variable-speed drive with one motion input and two outputs, as well as an angle input. The angle input varied the ratio (and direction) of coupling between the "motion" input and the outputs according to the sine and cosine of the input angle.

Although they did not accomplish any computation, electromechanical position servos were essential in mechanical analog computers of the "rotating-shaft" type for providing operating torque to the inputs of subsequent computing mechanisms, as well as driving output data-transmission devices such as large torque-transmitter synchros in naval computers.

Other readout mechanisms, not directly part of the computation, included internal odometer-like counters with interpolating drum dials for indicating internal variables, and mechanical multi-turn limit stops.

Considering that accurately controlled rotational speed in analog fire-control computers was a basic element of their accuracy, there was a motor with its average speed controlled by a balance wheel, hairspring, jeweled-bearing differential, a twin-lobe cam, and spring-loaded contacts (ship's AC power frequency was not necessarily accurate, nor dependable enough, when these computers were designed).

Electronic analog computers
Switching board of EAI 8800 analog computer (front view)

Electronic analog computers typically have front panels with numerous jacks (single-contact sockets) that permit patch cords (flexible wires with plugs at both ends) to create the interconnections that define the problem setup. In addition, there are precision high-resolution potentiometers (variable resistors) for setting up (and, when needed, varying) scale factors. In addition, there is usually a zero-center analog pointer-type meter for modest-accuracy voltage measurement. Stable, accurate voltage sources provide known magnitudes.

Typical electronic analog computers contain anywhere from a few to a hundred or more operational amplifiers ("op amps"), named because they perform mathematical operations. Op amps are a particular type of feedback amplifier with very high gain and stable input (low and stable offset). They are always used with precision feedback components that, in operation, all but cancel out the currents arriving from input components. The majority of op amps in a representative setup are summing amplifiers, which add and subtract analog voltages, providing the result at their output jacks. As well, op amps with capacitor feedback are usually included in a setup; they integrate the sum of their inputs with respect to time.

Integrating with respect to another variable is the nearly exclusive province of mechanical analog integrators; it is almost never done in electronic analog computers. However, given that a problem solution does not change with time, time can serve as one of the variables.

Other computing elements include analog multipliers, nonlinear function generators, and analog comparators.

Electrical elements such as inductors and capacitors used in electrical analog computers had to be carefully manufactured to reduce non-ideal effects. For example, in the construction of AC power network analyzers, one motive for using higher frequencies for the calculator (instead of the actual power frequency) was that higher-quality inductors could be more easily made. Many general-purpose analog computers avoided the use of inductors entirely, re-casting the problem in a form that could be solved using only resistive and capacitive elements, since high-quality capacitors are relatively easy to make.

The use of electrical properties in analog computers means that calculations are normally performed in real time (or faster), at a speed determined mostly by the frequency response of the operational amplifiers and other computing elements. In the history of electronic analog computers, there were some special high-speed types.

Nonlinear functions and calculations can be constructed to a limited precision (three or four digits) by designing function generators—special circuits of various combinations of resistors and diodes to provide the nonlinearity. Typically, as the input voltage increases, progressively more diodes conduct.

When compensated for temperature, the forward voltage drop of a transistor's base-emitter junction can provide a usably accurate logarithmic or exponential function. Op amps scale the output voltage so that it is usable with the rest of the computer.

Any physical process that models some computation can be interpreted as an analog computer. Some examples, invented for the purpose of illustrating the concept of analog computation, include using a bundle of spaghetti as a model of sorting numbers; a board, a set of nails, and a rubber band as a model of finding the convex hull of a set of points; and strings tied together as a model of finding the shortest path in a network. These are all described in Dewdney (1984).

Components
A 1960 Newmark analogue computer, made up of five units. This computer was used to solve differential equations and is currently housed at the Cambridge Museum of Technology.

Analog computers often have a complicated framework, but they have, at their core, a set of key components that perform the calculations. The operator manipulates these through the computer's framework.

Key hydraulic components might include pipes, valves and containers.

Key mechanical components might include rotating shafts for carrying data within the computer, miter gear differentials, disc/ball/roller integrators, cams (2-D and 3-D), mechanical resolvers and multipliers, and torque servos.

Key electrical/electronic components might include:

The core mathematical operations used in an electric analog computer are:

In some analog computer designs, multiplication is much preferred to division. Division is carried out with a multiplier in the feedback path of an Operational Amplifier.

Differentiation with respect to time is not frequently used, and in practice is avoided by redefining the problem when possible. It corresponds in the frequency domain to a high-pass filter, which means that high-frequency noise is amplified; differentiation also risks instability.

Limitations

In general, analog computers are limited by non-ideal effects. An analog signal is composed of four basic components: DC and AC magnitudes, frequency, and phase. The real limits of range on these characteristics limit analog computers. Some of these limits include the operational amplifier offset, finite gain, and frequency response, noise floor, non-linearities, temperature coefficient, and parasitic effects within semiconductor devices. For commercially available electronic components, ranges of these aspects of input and output signals are always figures of merit.

Decline

In the 1950s to 1970s, digital computers based on first vacuum tubes, transistors, integrated circuits and then micro-processors became more economical and precise. This led digital computers to largely replace analog computers. Even so, some research in analog computation is still being done. A few universities still use analog computers to teach control system theory. The American company Comdyna manufactured small analog computers.[36] At Indiana University Bloomington, Jonathan Mills has developed the Extended Analog Computer based on sampling voltages in a foam sheet.[37] At the Harvard Robotics Laboratory,[38] analog computation is a research topic. Lyric Semiconductor's error correction circuits use analog probabilistic signals. Slide rules are still popular among aircraft personnel.

Resurgence

With the development of very-large-scale integration (VLSI) technology, Yannis Tsividis' group at Columbia University has been revisiting analog/hybrid computers design in standard CMOS process. Two VLSI chips have been developed, an 80th-order analog computer (250 nm) by Glenn Cowan[39] in 2005[40] and a 4th-order hybrid computer (65 nm) developed by Ning Guo in 2015,[41] both targeting at energy-efficient ODE/PDE applications. Glenn's chip contains 16 macros, in which there are 25 analog computing blocks, namely integrators, multipliers, fanouts, few nonlinear blocks. Ning's chip contains one macro block, in which there are 26 computing blocks including integrators, multipliers, fanouts, ADCs, SRAMs and DACs. Arbitrary nonlinear function generation is made possible by the ADC+SRAM+DAC chain, where the SRAM block stores the nonlinear function data. The experiments from the related publications revealed that VLSI analog/hybrid computers demonstrated about 1–2 orders magnitude of advantage in both solution time and energy while achieving accuracy within 5%, which points to the promise of using analog/hybrid computing techniques in the area of energy-efficient approximate computing. In 2016, a team of researchers developed a compiler to solve differential equations using analog circuits.[42]

Analog computers are also used in neuromorphic computing, and in 2021 a group of researchers have shown that a specific type of artificial neural network called a spiking neural network was able to work with analog neuromorphic computers.[43]

Practical examples
X-15 simulator analog computer

These are examples of analog computers that have been constructed or practically used:

Analog (audio) synthesizers can also be viewed as a form of analog computer, and their technology was originally based in part on electronic analog computer technology. The ARP 2600's Ring Modulator was actually a moderate-accuracy analog multiplier.

The Simulation Council (or Simulations Council) was an association of analog computer users in US. It is now known as The Society for Modeling and Simulation International. The Simulation Council newsletters from 1952 to 1963 are available online and show the concerns and technologies at the time, and the common use of analog computers for missilry.[44]

See also
Wikimedia Commons has media related to Analog computers.

Notes
  1. "Gears of war: When mechanical analog computers ruled the waves". 18 March 2014. Archived from the original on 8 September 2018. Retrieved 14 June 2017.
  2. Johnston, Sean F. (2006). Holographic Visions: A History of New Science. OUP Oxford. p. 90. ISBN 978-0191513886.
  3. "The Antikythera Mechanism Research Project". 28 April 2008. Archived from the original on 28 April 2008. Retrieved 1 July 2007.
  4. Fuat Sezgin "Catalogue of the Exhibition of the Institute for the History of Arabic-Islamic Science (at the Johann Wolfgang Goethe University", Frankfurt, Germany) Frankfurt Book Fair 2004, pp. 35 & 38.
  5. François Charette, Archaeology: High tech from Ancient Greece, Nature 444, 551–552(30 November 2006), doi:10.1038/444551a
  6. Silvio A. Bedini, Francis R. Maddison (1966). "Mechanical Universe: The Astrarium of Giovanni de' Dondi", Transactions of the American Philosophical Society 56 (5), pp. 1–69.
  7. D. De S. Price (1984). "A History of Calculating Machines", IEEE Micro 4 (1), pp. 22–52.
  8. Tuncer Őren (2001). "Advances in Computer and Information Sciences: From Abacus to Holonic Agents", Turk J Elec Engin 9 (1), pp. 63–70 [64].
  9. Donald Routledge Hill (1985). "Al-Biruni's mechanical calendar", Annals of Science 42, pp. 139–163.
  10. "An Amazing Perpetual Calendar, Hidden in an Italian Chapel". Atlas Obscura. Retrieved 7 September 2020.
  11. Torres, Leonardo (10 October 1895). "Memória sobre las Máquinas Algébricas" (PDF). Revista de Obras Públicas (in Spanish) (28): 217–222.
  12. Leonardo Torres. Memoria sobre las máquinas algébricas: con un informe de la Real academia de ciencias exactas, fisicas y naturales, Misericordia, 1895.
  13. Thomas, Federico (1 August 2008). "A short account on Leonardo Torres' endless spindle". Mechanism and Machine Theory. IFToMM. 43 (8): 1055–1063. doi:10.1016/j.mechmachtheory.2007.07.003. hdl:10261/30460. ISSN 0094-114X.
  14. Ray Girvan, "The revealed grace of the mechanism: computing after Babbage" Archived November 3, 2012, at the Wayback Machine, Scientific Computing World, May/June 2003
  15. Clymer, Arthur Ben (1993). "The Mechanical Analog Computers of Hannibal Ford and William Newell" (PDF). Retrieved 11 February 2023.
  16. Thomas Parke Hughes Networks of power: electrification in Western society, 1880–1930 JHU Press, 1993 ISBN 0-8018-4614-5 page 376
  17. James E. Tomayko, Helmut Hoelzer's Fully Electronic Analog Computer; In: IEEE Annals of the History of Computing, Vol. 7, No. 3, pp. 227–240, July–Sept. 1985, doi:10.1109/MAHC.1985.10025
  18. Neufeld, Michael J. (2013). The Rocket and the Reich: Peenemunde and the Coming of the Ballistic Missile Era. Smithsonian Institution. p. 138. ISBN 9781588344663.
  19. Ulmann, Bernd (22 July 2013). Analog Computing. Walter de Gruyter. p. 38. ISBN 9783486755183.
  20. Neufeld (2013), p. 106.
  21. Tomayko, James E. (1 July 1985). "Helmut Hoelzer". IEEE Annals of the History of Computing. 7 (3): 227–240. doi:10.1109/MAHC.1985.10025. S2CID 15986944.
  22. Metropolis, N. "The Beginning of the Monte Carlo Method." Los Alamos Science, No. 15, p. 125
  23. Small, J. S. "The analogue alternative: The electronic analogue computer in Britain and the USA, 1930–1975" Psychology Press, 2001, p. 90
  24. Small, J. S. "The analogue alternative: The electronic analogue computer in Britain and the USA, 1930–1975" Psychology Press, 2001, p. 93
  25. Bissell, C. (1 February 2007). "Historical perspectives – The Moniac A Hydromechanical Analog Computer of the 1950s" (PDF). IEEE Control Systems Magazine. 27 (1): 69–74. doi:10.1109/MCS.2007.284511. ISSN 1066-033X. S2CID 37510407. Archived (PDF) from the original on 9 October 2022.
  26. "History – Accounts". me100.caltech.edu.
  27. Karplus, Walter J. (29 November 2017). "Analog simulation: solution of field problems". McGraw-Hill – via Google Books.
  28. Petersen, Julie K. (2003). Fiber optics illustrated dictionary. CRC Press. p. 441. ISBN 978-0-8493-1349-3.
  29. "Heathkit EC - 1 Educational Analog Computer". Computer History Museum. Archived from the original on 20 May 2010. Retrieved 9 May 2010.
  30. Practical Electronics, January 1968
  31. EPE Hybrid Computer - Part 1 (November 2002), Part 2 (December 2002), Everyday Practical Electronics
  32. "System Description EAI 8800 Scientific Computing System" (PDF). 1 May 1965. Archived (PDF) from the original on 9 October 2022. Retrieved 17 September 2019.
  33. Small, James S. (2001). The Analogue Alternative. The Electronic Analogue Computer in Britain and USA, 1930-1975. London: Routledge. pp. 119–178.
  34. Havranek, Bill (1 August 1966). The role of a hybrid computer in supersonic transport simulation. pp. 91–99. {{cite book}}: |work= ignored (help)
  35. "Basic Fire Control Mechanisms". maritime.org.
  36. "Analog Computers". Comdyna. Archived from the original on 1 December 2017. Retrieved 6 October 2008.
  37. "Kirchhoff-Lukasiewicz Machines".
  38. "Harvard Robotics Laboratory".
  39. "Glenn Cowan". Concordia.ca. Retrieved 5 February 2016.
  40. Cowan, G.E.R.; Melville, R.C.; Tsividis, Y. (1 February 2005). "A VLSI analog computer/Math co-processor for a digital computer". ISSCC. 2005 IEEE International Digest of Technical Papers. Solid-State Circuits Conference, 2005. Vol. 1. pp. 82–586. doi:10.1109/ISSCC.2005.1493879. ISBN 978-0-7803-8904-5. S2CID 38664036.
  41. Guo, Ning; Huang, Yipeng; Mai, Tao; Patil, S.; Cao, Chi; Seok, Mingoo; Sethumadhavan, S.; Tsividis, Y. (1 September 2015). "Continuous-time hybrid computation with programmable nonlinearities". ESSCIRC Conference 2015 - 41st European Solid-State Circuits Conference (ESSCIRC). pp. 279–282. doi:10.1109/ESSCIRC.2015.7313881. ISBN 978-1-4673-7470-5. S2CID 16523767.
  42. "Analog computing returns". 20 June 2016.
  43. Benjamin Cramer; Sebastian Billaudelle; Simeon Kanya; Aron Leibfried; Andreas Grübl; Vitali Karasenko; Christian Pehle; Korbinian Schreiber; Yannik Stradmann; Johannes Weis; Johannes Schemmel; View ORCID ProfileFriedemann Zenke (25 January 2022). "Surrogate gradients for analog neuromorphic computing". PNAS. 119 (4). Bibcode:2022PNAS..11909194C. doi:10.1073/pnas.2109194119. PMC 8794842. PMID 35042792.
  44. "Simulation Council newsletter". Archived from the original on 28 May 2013.

References
  • A.K. Dewdney. "On the Spaghetti Computer and Other Analog Gadgets for Problem Solving", Scientific American, 250(6):19–26, June 1984. Reprinted in The Armchair Universe, by A.K. Dewdney, published by W.H. Freeman & Company (1988), ISBN 0-7167-1939-8.
  • Universiteit van Amsterdam Computer Museum. (2007). Analog Computers.
  • Jackson, Albert S., "Analog Computation". London & New York: McGraw-Hill, 1960. OCLC 230146450
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.