Anne's theorem

A point L lies on the Newton line if the two sums of the areas of opposing triangles are equal, according to Anne's theorem.

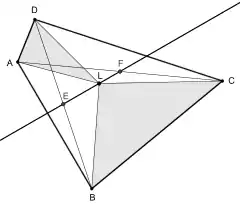
The theorem is stated as follows: Let ABCD be a convex quadrilateral with diagonals AC and BD, that is not a parallelogram. Furthermore, let E and F be the midpoints of the diagonals, and let L be an arbitrary point in the interior of ABCD, resulting in that L forms four triangles with the edges of ABCD. If the two sums of areas of opposite triangles are equal:

$${\displaystyle \left|\triangle BCL\right|+\left|\triangle DAL\right|=\left|\triangle LAB\right|+\left|\triangle DLC\right|,}$$

then the point L is located on the Newton line, that is the line which connects E and F.[1][2]

For a parallelogram, the Newton line does not exist since both midpoints of the diagonals coincide with point of intersection of the diagonals. Moreover, the area identity of the theorem holds in this case for any inner point of the quadrilateral.

The converse of Anne's theorem is true as well, that is for any point on the Newton line which is an inner point of the quadrilateral, the area identity holds.

• Newton's and Léon Anne's Theorems at cut-the-knot.org
• Andrew Jobbings: The Converse of Leon Anne's Theorem Archived 2014-03-04 at the Wayback Machine
• Weisstein, Eric W. "Leon Anne's Theorem". MathWorld.