Anthropomorphic polygon
In geometry, an anthropomorphic polygon is a simple polygon with precisely two ears and one mouth. That is, for exactly three polygon vertices, the line segment connecting the two neighbors of the vertex does not cross the polygon. For two of these vertices (the ears) the line segment connecting the neighbors forms a diagonal of the polygon, contained within the polygon. For the third vertex (the mouth) the line segment connecting the neighbors lies outside the polygon, forming the entrance to a concavity of the polygon.[1]
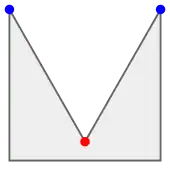
Every simple polygon has at least two ears (this is the two ears theorem) and every non-convex simple polygon has at least one mouth, so in some sense the anthropomorphic polygons are the simplest possible non-convex simple polygons.[1]
It is possible to recognize anthropomorphic polygons in linear time.[2]
References
- Toussaint, Godfried (1991), "Anthropomorphic polygons", The American Mathematical Monthly, 98 (1): 31–35, doi:10.2307/2324033, JSTOR 2324033, MR 1083611.
- Shermer, T.; Toussaint, G. T. (1989), "Anthropomorphic polygons can be recognized in linear time", in Janicki, Ryszard; Koczkodaj, Waldemar W. (eds.), Proceedings of the International Conference on Computing and Information, North-Holland, pp. 117–123.