Antiparallel lines

In geometry, two lines ${\displaystyle l_{1}}$ and ${\displaystyle l_{2}}$ are antiparallel with respect to a given line ${\displaystyle m}$ if they each make congruent angles with ${\displaystyle m}$ in opposite senses. More generally, lines ${\displaystyle l_{1}}$ and ${\displaystyle l_{2}}$ are antiparallel with respect to another pair of lines ${\displaystyle m_{1}}$ and ${\displaystyle m_{2}}$ if they are antiparallel with respect to the angle bisector of ${\displaystyle m_{1}}$ and ${\displaystyle m_{2}.}$

In any cyclic quadrilateral, any two opposite sides are antiparallel with respect to the other two sides.

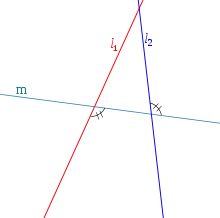Lines ${\displaystyle l_{1}}$ and ${\displaystyle l_{2}}$ are antiparallel with respect to the line ${\displaystyle m}$ if they make the same angle with ${\displaystyle m}$ in the opposite senses.	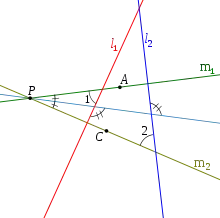Two lines ${\displaystyle l_{1}}$ and ${\displaystyle l_{2}}$ are antiparallel with respect to the sides of an angle if they make the same angle ${\displaystyle \angle APC}$ in the opposite senses with the bisector of that angle.
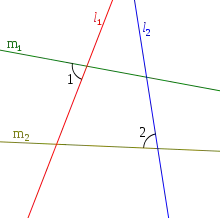Given two lines ${\displaystyle m_{1}}$ and ${\displaystyle m_{2}}$, lines ${\displaystyle l_{1}}$ and ${\displaystyle l_{2}}$ are antiparallel with respect to 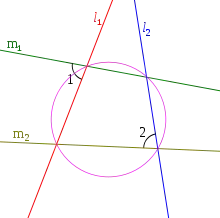${\displaystyle m_{1}}$ and ${\displaystyle m_{2}}$ if ${\displaystyle \angle 1=\angle 2}$.	In any quadrilateral inscribed in a circle, any two opposite sides are antiparallel with respect to the other two sides.