Aubry–André model

Aubry-André metal-insulator transition, inverse of localization length ${\displaystyle l_{\rm {loc}}}$ as a function of energy ratios ${\displaystyle \lambda /J}$.

Aubry–André model defines a periodic potential over a one-dimensional lattice with hopping between nearest neighbors sites with no interactions. In tight-binding,[2] the on-site energies of Aubry-André potential have a periodicity that is incommensurate with the periodicity of the lattice. The potential can be written as

${\displaystyle V=\sum _{n}\epsilon _{n}|n\rangle \langle n|}$,

where the sum goes over all sites ${\displaystyle n}$, ${\displaystyle |n\rangle }$ is a Wannier state on lattice site ${\displaystyle n}$ and the on-site energies are given by

${\displaystyle \epsilon _{n}=\lambda \cos(2\pi \beta n+\varphi )}$.

where ${\displaystyle \lambda }$ is the disorder strength, ${\displaystyle \varphi }$ is a phase and ${\displaystyle \beta }$ is the periodicity of the potential.

The full Hamiltonian can be written as

${\displaystyle H=-J\sum _{n}(|n\rangle \langle n+1|+|n+1\rangle \langle n|)+V}$,

where ${\displaystyle J}$ is the hopping constant. This Hamiltonian is self-dual as it retains the same form after a Fourier transformation.[3]

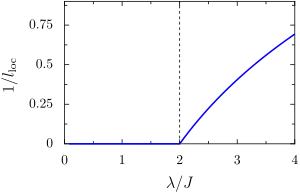
For special values of ${\displaystyle \beta }$ the system can demonstrate localization. For the case where ${\displaystyle \varphi =0}$ and ${\displaystyle \beta =(1+{\sqrt {5}})/2}$ (golden ratio), Aubry and André showed that if ${\displaystyle \lambda >2J}$, then the eigenmodes are exponentially localized, as in the Anderson model. For ${\displaystyle \lambda <2J}$, the eigenmodes are extended plane waves. This limit between the two behaviors ${\displaystyle \lambda =2J}$ is called the localization transition or the Aubry-André transition.[4] For finite chains, the periodicity of the potential can also be chosen to be the ratio ${\displaystyle \beta =P/Q}$, with primes ${\displaystyle P}$ and ${\displaystyle Q}$ larger than number of sites in the chain.[3]

In the Aubry-André model, the energy spectrum ${\displaystyle E_{n}}$ as function of ${\displaystyle \beta }$, is given by the almost Mathieu equation

${\displaystyle E_{n}\psi _{n}=-J(\psi _{n+1}+\psi _{n-1})+\epsilon _{n}\psi _{n}}$,

related to Harper equation (${\displaystyle \lambda =2J}$) that leads to a fractal spectrum known as the Hofstadter's butterfly, which describes the motion of an electron in a two-dimensional lattice under a magnetic field.[3][4]

IN 2009, Y. Lahini et al. presented one of the first experimental realizations of the Aubry-André model in photonic lattices.[5]