Axial current

According to Noether's theorem, each symmetry of a system is associated a conserved quantity.[1][2] For example, the rotational invariance of a system implies the conservation of its angular momentum, or spacetime invariance implies the conservation of energy–momentum. In quantum field theory, internal symmetries also result in conserved quantities. For example, the U(1) gauge transformation of QED implies the conservation of the electric charge. Likewise, if a theory possesses an internal chiral or axial symmetry, there will be a conserved quantity, which is called the axial charge. Further, just as the motion of an electrically charged particle produces an electric current, a moving axial charge constitutes an axial current.

The axial current resulting from the motion of an axially charged moving particle is formally defined as ${\displaystyle j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi }$, where ${\displaystyle \psi }$ is the particle field represented by Dirac spinor (since the particle is typically a spin-1/2 fermion) and ${\displaystyle \gamma ^{5}}$ and ${\displaystyle \gamma ^{\mu }}$ are the Dirac gamma matrices.[3]

For comparison, the electromagnetic current produced by an electrically charged moving particle is ${\displaystyle j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi }$.

As explained above, the axial current is simply the equivalent of the electromagnetic current for the axial symmetry instead of the U(1) symmetry. Another perspective is given by recalling that the chiral symmetry is the invariance of the theory under the field rotation ${\displaystyle \psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}}$  and  ${\displaystyle \psi _{\rm {R}}\rightarrow \psi _{\rm {R}}}$ (or alternatively ${\displaystyle \psi _{\rm {L}}\rightarrow \psi _{\rm {L}}}$  and   ${\displaystyle \psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}}$), where ${\displaystyle \psi _{\rm {L}}}$ denotes a left-handed field and ${\displaystyle \psi _{\rm {R}}}$ a right-handed one. From this as well as the fact that ${\displaystyle \psi =\psi _{\rm {L}}+\psi _{\rm {R}}}$ and the definition of ${\displaystyle j_{5}^{\mu }}$ above, one sees that the axial current is the difference between the current due to left-handed fermions and that from right-handed ones, whilst the electromagnetic current is the sum.

Chiral symmetry is exhibited by vector gauge theories with massless fermions. Since there is no known massless fermion in nature, chiral symmetry is at best an approximate symmetry in fundamental theories, and the axial current is not conserved. (Note: this explicit breaking of the chiral symmetry by non-zero masses is not to be confused with the spontaneous chiral symmetry breaking that plays a dominant role in hadronic physics.) An important consequence of such non-conservation is the neutral pion decay and the chiral anomaly,[4] which is directly related to the pion decay width.[5][6]

The axial current is an important part of the formalism describing high-energy scattering reactions. In such reaction, two particles scatter off each other by exchanging a force boson, e.g., a photon for electromagnetic scattering (see the figure).

A Feynman diagram of scattering between two electrons by emission of a virtual photon.

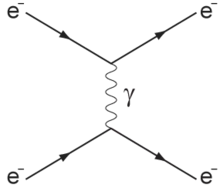
The cross-section for such reaction is proportional to the square of the scattering amplitude, which in turn is given by the product of boson propagator times the two currents associated with the motions two colliding particles.[7] Therefore, currents (axial or electromagnetic) are one of the two essential ingredients needed to compute high-energy scattering, the other being the boson propagator.

In electron–nucleon scattering (or more generally, charged lepton–hadron/nucleus scattering) the axial current yields the spin-dependent part of the cross-section.[8] (The spin-average part of the cross-section comes from the electromagnetic current.[7])

In neutrino–nucleon scattering, neutrinos couple only via the axial current, thus accessing different nucleon structure information than with charged leptons.[9]

Neutral pions also couple only via the axial current because pions are pseudoscalar particles and, to produce amplitudes (scalar quantities), a pion must couple to another pseudoscalar object like the axial current. (Charged pions can also couple via the electromagnetic current.)

• Chiral anomaly
• QCD
• Chiral symmetry breaking
• Chiral perturbation theory
• Chiral magnetic effect
• Parity (physics)