Barycentric subdivision
In mathematics, the barycentric subdivision is a standard way to subdivide a given simplex into smaller ones. Its extension on simplicial complexes is a canonical method to refine them. Therefore, the barycentric subdivision is an important tool in algebraic topology.
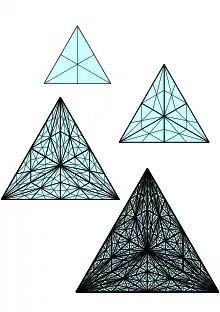
Motivation
The barycentric subdivision is an operation on simplicial complexes. In algebraic topology it is sometimes useful to replace the original spaces with simplicial complexes via triangulations: The substitution allows to assign combinatorial invariants as the Euler characteristic to the spaces. One can ask if there is an analogous way to replace the continuous functions defined on the topological spaces by functions that are linear on the simplices and which are homotopic to the original maps (see also simplicial approximation). In general, such an assignment requires a refinement of the given complex, meaning, one replaces bigger simplices by a union of smaller simplices. A standard way to effectuate such a refinement is the barycentric subdivision. Moreover, barycentric subdivision induces maps on homology groups and is helpful for computational concerns, see Excision and Mayer-Vietoris-sequence.
Definition
Subdivision of simplicial complexes
Let be a geometric simplicial complex. A complex is said to be a subdivision of if
- each simplex of is contained in a simplex of
- each simplex of is a finite union of simplices of
These conditions imply that and equal as sets and as topological spaces, only the simplicial structure changes.[1]

Barycentric subdivision of a simplex
For a simplex spanned by points , the barycenter is defined to be the point . To define the subdivision, we will consider a simplex as a simplicial complex that contains only one simplex of maximal dimension, namely the simplex itself. The barycentric subdivision of a simplex can be defined inductively by its dimension.
For points, i.e. simplices of dimension 0, the barycentric subdivision is defined as the point itself.
Suppose then for a simplex of dimension that its faces of dimension are already divided. Therefore, there exist simplices covering . The barycentric subdivision is then defined to be the geometric simplicial complex whose maximal simplices of dimension are each a convex hulls of for one pair for some , so there will be simplices covering .
One can generalize the subdivision for simplicial complexes whose simplices are not all contained in a single simplex of maximal dimension, i.e. simplicial complexes that do not correspond geometrically to one simplex. This can be done by effectuating the steps described above simultaneously for every simplex of maximal dimension. The induction will then be based on the -th skeleton of the simplicial complex. It allows effectuating the subdivision more than once.[2]
Barycentric subdivision of a convex polytope

The operation of barycentric subdivision can be applied to any convex polytope of any dimension, producing another convex polytope of the same dimension.[3] In this version of barycentric subdivision, it is not necessary for the polytope to form a simplicial complex: it can have faces that are not simplices. This is the dual operation to omnitruncation.[4] The vertices of the barycentric subdivision correspond to the faces of all dimensions of the original polytope. Two vertices are adjacent in the barycentric subdivision when they correspond to two faces of different dimensions with the lower-dimensional face included in the higher-dimensional face. The facets of the barycentric subdivision are simplices, corresponding to the flags of the original polytope.
For instance, the barycentric subdivision of a cube, or of a regular octahedron, is the disdyakis dodecahedron.[5] The degree-6, degree-4, and degree-8 vertices of the disdyakis dodecahedron correspond to the vertices, edges, and square facets of the cube, respectively.
Properties
Mesh
Let a simplex and define . One way to measure the mesh of a geometric, simplicial complex is to take the maximal diameter of the simplices contained in the complex. Let be an - dimensional simplex that comes from the covering of obtained by the barycentric subdivision. Then, the following estimation holds:
. Therefore, by applying barycentric subdivision sufficiently often, the largest edge can be made as small as desired.[6]
Homology
For some statements in homology-theory one wishes to replace simplicial complexes by a subdivision. On the level of simplicial homology groups one requires a map from the homology-group of the original simplicial complex to the groups of the subdivided complex. Indeed it can be shown that for any subdivision of a finite simplicial complex there is a unique sequence of maps between the homology groups such that for each in the maps fulfills and such that the maps induces endomorphisms of chain complexes. Moreover, the induced map is an isomorphism: Subdivision does not change the homology of the complex.[1]
To compute the singular homology groups of a topological space one considers continuous functions where denotes the -dimensional-standard-simplex. In an analogous way as described for simplicial homology groups, barycentric subdivision can be interpreted as an endomorphism of singular chain complexes. Here again, there exists a subdivision operator sending a chain to a linear combination where the sum runs over all simplices that appear in the covering of by barycentric subdivision, and for all of such . This map also induces an automorphism of chain complexes.[7]
Applications
The barycentric subdivision can be applied on whole simplicial complexes as in the simplicial approximation theorem or it can be used to subdivide geometric simplices. Therefore it is crucial for statements in singular homology theory, see Mayer-Vietoris-sequence and excision.
Simplicial approximation
Let , be abstract simplicial complexes above sets , . A simplicial map is a function which maps each simplex in onto a simplex in . By affin-linear extension on the simplices, induces a map between the geometric realizations of the complexes. Each point in a geometric complex lies in the inner of exactly one simplex, its support. Consider now a continuous map . A simplicial map is said to be a simplicial approximation of if and only if each is mapped by onto the support of in . If such an approximation exists, one can construct a homotopy transforming into by defining it on each simplex; there, it always exists, because simplices are contractible.
The simplicial approximation theorem guarantees for every continuous function the existence of a simplicial approximation at least after refinement of , for instance by replacing by its iterated barycentric subdivision.[8] The theorem plays an important role for certain statements in algebraic topology in order to reduce the behavior of continuous maps on those of simplicial maps, as for instance in Lefschetz's fixed-point theorem.
Lefschetz's fixed-point theorem
The Lefschetz number is a useful tool to find out whether a continuous function admits fixed-points. This data is computed as follows: Suppose that and are topological spaces that admit finite triangulations. A continuous map induces homomorphisms between its simplicial homology groups with coefficients in a field . These are linear maps between - vectorspaces, so their trace can be determined and their alternating sum
is called the Lefschetz number of . If , this number is the Euler characteristic of . The fixpoint theorem states that whenever , has a fixed-point. In the proof this is first shown only for simplicial maps and then generalized for any continuous functions via the approximation theorem.
Now, Brouwer's fixpoint theorem is a special case of this statement. Let is an endomorphism of the unit-ball. For all its homology groups vanish, and is always the identity, so , so has a fixpoint.[9]
Mayer-Vietoris-Sequence
The Mayer- Vietoris- Sequence is often used to compute singular homology groups and gives rise to inductive arguments in topology. The related statement can be formulated as follows:
Let an open cover of the topological space .
There is an exact sequence
where we consider singular homology groups, are embeddings and denotes the direct sum of abelian groups.
For the construction of singular homology groups one considers continuous maps defined on the standard simplex . An obstacle in the proof of the theorem are maps such that their image is nor contained in neither in . This can be fixed using the subdivision operator: By considering the images of such maps as the sum of images of smaller simplices, lying in or one can show that the inclusion induces an isomorphism on homology which is needed to compare the homology groups.[10]
Excision
Excision can be used to determine relative homology groups. It allows in certain cases to forget about subsets of topological spaces for their homology groups and therefore simplifies their computation:
Let be a topological space and let be subsets, where is closed such that . Then the inclusion induces an isomorphism for all
Again, in singular homology, maps may appear such that their image is not part of the subsets mentioned in the theorem. Analogously those can be understood as a sum of images of smaller simplices obtained by the barycentric subdivision.[11]
References
- James R. Munkres, Elements of algebraic topology (in German), Menlo Park, Calif., p. 96, ISBN 0-201-04586-9
- James R. Munkres, Elements of algebraic topology (in German), Menlo Park, Calif., pp. 85 f, ISBN 0-201-04586-9
- Ewald, G.; Shephard, G. C. (1974), "Stellar subdivisions of boundary complexes of convex polytopes", Mathematische Annalen, 210: 7–16, doi:10.1007/BF01344542, MR 0350623
- Matteo, Nicholas (2015), Convex Polytopes and Tilings with Few Flag Orbits (Doctoral dissertation), Northeastern University, ProQuest 1680014879 See p. 22, where the omnitruncation is described as a "flag graph".
- Langer, Joel C.; Singer, David A. (2010), "Reflections on the lemniscate of Bernoulli: the forty-eight faces of a mathematical gem", Milan Journal of Mathematics, 78 (2): 643–682, doi:10.1007/s00032-010-0124-5, MR 2781856
- Hatcher, Allen (2001), Algebraic Topology (PDF), p. 120
- Hatcher (2001), pp. 122 f.
- Ralph Stöcker, Heiner Zieschang, Algebraische Topologie (in German) (2. überarbeitete ed.), Stuttgart: B.G. Teubner, p. 81, ISBN 3-519-12226-X
- Bredon, Glen E., Springer Verlag (ed.), Topology and Geometry (in German), Berlin/ Heidelberg/ New York, pp. 254 f, ISBN 3-540-97926-3
- Hatcher (2001), p. 149.
- Hatcher (2001), p. 119.