Boundary conditions in fluid dynamics

Showing inlet flow velocity in a pipe

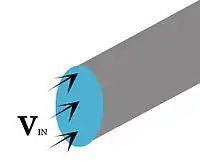
In inlet boundary conditions, the distribution of all flow variables needs to be specified at inlet boundaries mainly flow velocity.[1] This type of boundary conditions are common and specified mostly where inlet flow velocity is known.

Showing outlet flow velocity in a pipe

In outlet boundary conditions, the distribution of all flow variables needs to be specified, mainly flow velocity. This can be thought as a conjunction to inlet boundary condition. This type of boundary conditions is common and specified mostly where outlet velocity is known.[1] The flow attains a fully developed state where no change occurs in the flow direction when the outlet is selected far away from the geometrical disturbances. In such region, an outlet could be outlined and the gradient of all variables could be equated to zero in the flow direction except pressure.

Showing wall boundary condition

The most common boundary that comes upon in confined fluid flow problems is the wall of the conduit. The appropriate requirement is called the no-slip boundary condition, wherein the normal component of velocity is fixed at zero, and the tangential component is set equal to the velocity of the wall.[1] It may run counter to intuition, but the no-slip condition has been firmly established in both experiment and theory, though only after decades of controversy and debate.[2]

$${\displaystyle V_{\text{normal}}=0}$$

$${\displaystyle V_{\text{tangential}}=V_{\text{wall}}}$$

Heat transfer through the wall can be specified or if the walls are considered adiabatic, then heat transfer across the wall is set to zero.

$${\displaystyle Q_{\text{Adiabatic Walls}}=0}$$

Showing constant pressure boundary condition

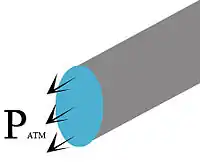
This type of boundary condition is used where boundary values of pressure are known and the exact details of the flow distribution are unknown. This includes pressure inlet and outlet conditions mainly. Typical examples that utilize this boundary condition include buoyancy driven flows, internal flows with multiple outlets, free surface flows and external flows around objects.[1] An example is flow outlet into atmosphere where pressure is atmospheric.

Showing axisymmetric boundary condition

In this boundary condition, the model is axisymmetric with respect to the main axis such that at a particular r = R, all θs and each z = Z-slice, each flow variable has the same value.[3] A good example is the flow in a circular pipe where the flow and pipe axes coincide.

${\displaystyle V_{r}(R,\theta ,Z)=Constant}$ ${\displaystyle (r=R,\theta ,Z)}$

Showing symmetric boundary condition

In this boundary condition, it is assumed that on the two sides of the boundary, same physical processes exist.[4] All the variables have same value and gradients at the same distance from the boundary. It acts as a mirror that reflects all the flow distribution to the other side.[5] The conditions at symmetric boundary are no flow across boundary and no scalar flux across boundary.

A good example is of a pipe flow with a symmetric obstacle in the flow. The obstacle divides the upper flow and lower flow as mirrored flow.

A quarter showing cyclic boundary condition

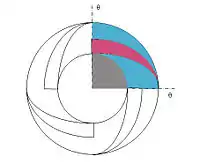
A periodic or cyclic boundary condition arises from a different type of symmetry in a problem. If a component has a repeated pattern in flow distribution more than twice, thus violating the mirror image requirements required for symmetric boundary condition. A good example would be swept vane pump (Fig.),[6] where the marked area is repeated four times in r-theta coordinates. The cyclic-symmetric areas should have the same flow variables and distribution and should satisfy that in every Z-slice.[1]

Wikimedia Commons has media related to Boundary conditions in computational fluid dynamics.

• Flow conditioning
• Initial value problem

• Versteeg (1995). "Chapter 9". An Introduction to Computational Fluid Dynamics The Finite Volume Method, 2/e. Longman Scientific & Technical. pp. 192–206. ISBN 0-582-21884-5.