Cantellation (geometry)

In geometry, a cantellation is a 2nd-order truncation in any dimension that bevels a regular polytope at its edges and at its vertices, creating a new facet in place of each edge and of each vertex. Cantellation also applies to regular tilings and honeycombs. Cantellating a polyhedron is also rectifying its rectification.

A cantellated cube - Red faces are reduced. Edges are bevelled, forming new yellow square faces. Vertices are truncated, forming new blue triangle faces.
A cantellated cubic honeycomb - Purple cubes are cantellated. Edges are bevelled, forming new blue cubic cells. Vertices are truncated, forming new red rectified cube cells.

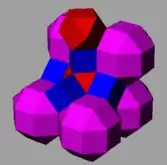
Cantellation (for polyhedra and tilings) is also called expansion by Alicia Boole Stott: it corresponds to moving the faces of the regular form away from the center, and filling in a new face in the gap for each opened edge and for each opened vertex.

Notation

A cantellated polytope is represented by an extended Schläfli symbol t0,2{p,q,...} or r or rr{p,q,...}.

For polyhedra, a cantellation offers a direct sequence from a regular polyhedron to its dual.

Example: cantellation sequence between cube and octahedron:

Example: a cuboctahedron is a cantellated tetrahedron.

For higher-dimensional polytopes, a cantellation offers a direct sequence from a regular polytope to its birectified form.

Examples: cantellating polyhedra, tilings
Regular polyhedra, regular tilings
Form Polyhedra Tilings
Coxeter rTT rCO rID rQQ rHΔ
Conway
notation		 eT eC = eO eI = eD eQ eH = eΔ
Polyhedra to
be expanded		 Tetrahedron Cube or
octahedron		 Icosahedron or
dodecahedron		 Square tiling Hexagonal tiling
Triangular tiling
Image
Animation
Uniform polyhedra or their duals
Coxeter rrt{2,3} rrs{2,6} rrCO rrID
Conway
notation		 eP3 eA4 eaO = eaC eaI = eaD
Polyhedra to
be expanded		 Triangular prism or
triangular bipyramid		 Square antiprism or
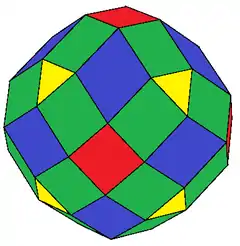
tetragonal trapezohedron		 Cuboctahedron or
rhombic dodecahedron		 Icosidodecahedron or
rhombic triacontahedron
Image
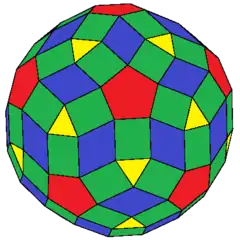Animation

See also

References
  • Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
    • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.