Cartesian parallel manipulators

In robotics, Cartesian parallel manipulators are manipulators that move a platform using parallel-connected kinematic linkages ('limbs') lined up with a Cartesian coordinate system. Multiple limbs connect the moving platform to a base. Each limb is driven by a linear actuator and the linear actuators are mutually perpendicular. The term 'parallel' here refers to the way that the kinematic linkages are put together, it does not connote geometrically parallel; i.e., equidistant lines.

Context

Generally, manipulators (also called 'robots' or 'mechanisms') are mechanical devices that position and orientate objects. The position of an object in three-dimensional (3D) space can be specified by three numbers X, Y, Z known as 'coordinates.' In a Cartesian coordinate system (named after René Descartes who introduced analytic geometry, the mathematical basis for controlling manipulators) the coordinates specify distances from three mutually perpendicular reference planes.  The orientation of an object in 3D can be specified by three additional numbers corresponding to the orientation angles.  The first  manipulators were developed after World War II for the Argonne National Laboratory to safely handle highly radioactive material remotely.  The first numerically controlled manipulators (NC machines) were developed by Parsons Corp. and the MIT Servomechanisms Laboratory, for milling applications.  These machines position a cutting tool relative to a Cartesian coordinate system using three mutually perpendicular linear actuators (prismatic P joints), with (PP)P joint topology.  The first industrial robot,[1] Unimate, was invented in the 1950s. Its control axes correspond to a spherical coordinate system, with RRP joint topology composed of two revolute R joints in series with a prismatic P joint.  Most industrial robots today are articulated robots composed of a serial chain of revolute R joints RRRRRR.

Description

Cartesian parallel manipulators are in the intersection of two broader categories of manipulators: Cartesian and parallel. Cartesian manipulators are driven by mutually perpendicular linear actuators. They generally have a one-to-one correspondence between the linear positions of the actuators and the X, Y, Z position coordinates of the moving platform, making them easy to control. Furthermore, Cartesian manipulators do not change the orientation of the moving platform. Most commonly, Cartesian manipulators are serial-connected; i.e., they consist of a single kinematic linkage chain, i.e. the first linear actuator moves the second one and so on. On the other hand, Cartesian parallel manipulators are parallel-connected, i.e. they consist of multiple kinematic linkages. Parallel-connected manipulators have innate advantages[2] in terms of stiffness,[3] precision,[4] dynamic performance[5] [6] and in supporting heavy loads.[7]

Configurations

Various types of Cartesian parallel manipulators are summarized here. Only fully parallel-connected mechanisms are included; i.e., those having the same number of limbs as degrees of freedom of the moving-platform, with a single actuator per limb.

Multipteron family

Members of the Multipteron [8] family of manipulators have either 3, 4, 5 or 6 degrees of freedom (DoF). The Tripteron 3-DoF member has three translation degrees of freedom 3T DoF, with the subsequent members of the Multipteron family each adding a rotational R degree of freedom. Each member of the family has mutually perpendicular linear actuators connected to a fixed base. The moving platform is typically attached to the linear actuators through three geometrically parallel revolute R joints. See Kinematic pair for a description of shorthand joint notation used to describe manipulator configurations, like revolute R joint for example.

Tripteron
Tripteron

The 3-DoF Tripteron[9] [10] [11] [12][13] member of the Multipteron family has three parallel-connected kinematic chains consisting of a linear actuator (active prismatic P joint) in series with three revolute R joints 3(PRRR). Similar manipulators, with three parallelogram Pa limbs 3(PRPaR) are the Orthoglide[14] [15] and Parallel cube-manipulator.[16] The Pantepteron[17] is also similar to the Tripteron, with pantograph linkages to speed up the motion of the platform.

Qudrupteron
Quadrupteron

The 4-DoF Qudrupteron[18] has 3T1R DoF with (3PRRU)(PRRR) joint topology.

Pentapteron

The 5-DoF Pentateron[19] has 3T2R DoF with 5(PRRRR) joint topology.

Hexapteron

The 6-DoF Hexapteron[20] has 3T3R DoF with 6(PCRS) joint topology, with cylindrical C and spherical S joints.

Isoglide

The Isoglide family[21] [22][23][24] includes many different Cartesian parallel manipulators from 2-6 DoF.

Xactuator
Xactuator

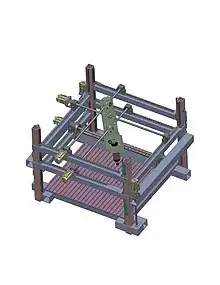
The 4-DoF or 5-DoF Coupled Cartesian manipulators family[25] are gantry type Cartesian parallel manipulators with 2T2R DoF or 3T2R DoF.

References
  1. George C Devol, Programmed article transfer, US patent 2988237, June 13, 1961. 
  2. Z. Pandilov, V. Dukovski, Comparison of the characteristics between serial and parallel robots, Acta Technica Corviniensis-Bulletin of Engineering, Volume 7, Issue 1, Pages 143-160
  3. Geldart, M; Webb, P; Larsson, H; Backstrom, M; Gindy, N; Rask, K (2003). "A direct comparison of the machining performance of a variax 5 axis parallel kinetic machining centre with conventional 3 and 5 axis machine tools". International Journal of Machine Tools and Manufacture. 43 (11): 1107–1116. doi:10.1016/s0890-6955(03)00119-6. ISSN 0890-6955.
  4. "Vibration control for precision manufacturing using piezoelectric actuators". Precision Engineering. 20 (2): 151. 1997. doi:10.1016/s0141-6359(97)81235-4. ISSN 0141-6359.
  5. R. Clavel, inventor, S.A. SovevaSwitzerland, assignee. Device for the movement and positioning of an element in space, USA patent number, 4,976,582 (1990)
  6. Prempraneerach, Pradya (2014). "Delta parallel robot workspace and dynamic trajectory tracking of delta parallel robot". 2014 International Computer Science and Engineering Conference (ICSEC). IEEE. pp. 469–474. doi:10.1109/icsec.2014.6978242. ISBN 978-1-4799-4963-2. S2CID 14227646.
  7.    Stewart D. A Platform with Six Degrees of Freedom. Proceedings of the Institution of Mechanical Engineers. 1965;180(1):371-386. doi:10.1243/PIME_PROC_1965_180_029_02  
  8. Gosselin, Clement M.; Masouleh, Mehdi Tale; Duchaine, Vincent; Richard, Pierre-Luc; Foucault, Simon; Kong, Xianwen (2007). "Parallel Mechanisms of the Multipteron Family: Kinematic Architectures and Benchmarking". Proceedings 2007 IEEE International Conference on Robotics and Automation. IEEE. pp. 555–560. doi:10.1109/robot.2007.363045. ISBN 978-1-4244-0602-9. S2CID 5755981.
  9. Gosselin, C. M., and Kong, X., 2004, “Cartesian Parallel Manipulators,” U.S. Patent No. 6,729,202
  10. Xianwen Kong, Clément M. Gosselin, Kinematics and Singularity Analysis of a Novel Type of 3-CRR 3-DOF Translational Parallel Manipulator, The International Journal of Robotics Research Vol. 21, No. 9, September 2002, pp. 791-7
  11. Kong, Xianwen; Gosselin, Clément M. (2002), "Type Synthesis of Linear Translational Parallel Manipulators", Advances in Robot Kinematics, Dordrecht: Springer Netherlands, pp. 453–462, doi:10.1007/978-94-017-0657-5_48, ISBN 978-90-481-6054-9, retrieved 2020-12-14
  12. Kim, Han Sung; Tsai, Lung-Wen (2002), "Evaluation of a Cartesian Parallel Manipulator", Advances in Robot Kinematics, Dordrecht: Springer Netherlands, pp. 21–28, doi:10.1007/978-94-017-0657-5_3, ISBN 978-90-481-6054-9, retrieved 2020-12-14
  13. Elkady, Ayssam; Elkobrosy, Galal; Hanna, Sarwat; Sobh, Tarek (2008-04-01), "Cartesian Parallel Manipulator Modeling, Control and Simulation", Parallel Manipulators, towards New Applications, I-Tech Education and Publishing, doi:10.5772/5435, ISBN 978-3-902613-40-0
  14. Wenger, P.; Chablat, D. (2000), "Kinematic Analysis of a New Parallel Machine Tool: The Orthoglide", Advances in Robot Kinematics, Dordrecht: Springer Netherlands, pp. 305–314, doi:10.1007/978-94-011-4120-8_32, ISBN 978-94-010-5803-2, S2CID 5485837, retrieved 2020-12-14
  15. Chablat, D.; Wenger, P. (2003). "Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the orthoglide". IEEE Transactions on Robotics and Automation. 19 (3): 403–410. arXiv:0708.3381. doi:10.1109/tra.2003.810242. ISSN 1042-296X. S2CID 3263909.
  16. Liu, Xin-Jun; Jeong, Jay il; Kim, Jongwon (2003-10-24). "A three translational DoFs parallel cube-manipulator". Robotica. 21 (6): 645–653. doi:10.1017/s0263574703005198. ISSN 0263-5747. S2CID 35529910.
  17. Briot, S.; Bonev, I. A. (2009-01-06). "Pantopteron: A New Fully Decoupled 3DOF Translational Parallel Robot for Pick-and-Place Applications". Journal of Mechanisms and Robotics. 1 (2). doi:10.1115/1.3046125. ISSN 1942-4302.
  18. Gosselin, C (2009-01-06). "Compact dynamic models for the tripteron and quadrupteron parallel manipulators". Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. 223 (1): 1–12. doi:10.1243/09596518jsce605. ISSN 0959-6518. S2CID 61817314.
  19. Gosselin, Clement M.; Masouleh, Mehdi Tale; Duchaine, Vincent; Richard, Pierre-Luc; Foucault, Simon; Kong, Xianwen (2007). "Parallel Mechanisms of the Multipteron Family: Kinematic Architectures and Benchmarking". Proceedings 2007 IEEE International Conference on Robotics and Automation. IEEE. pp. 555–560. doi:10.1109/robot.2007.363045. ISBN 978-1-4244-0602-9. S2CID 5755981.
  20. Seward, Nicholas; Bonev, Ilian A. (2014). "A new 6-DOF parallel robot with simple kinematic model". 2014 IEEE International Conference on Robotics and Automation (ICRA). IEEE. pp. 4061–4066. doi:10.1109/icra.2014.6907449. ISBN 978-1-4799-3685-4. S2CID 18895630.
  21. Gogu, Grigore (2004). "Structural synthesis of fully-isotropic translational parallel robots via theory of linear transformations". European Journal of Mechanics - A/Solids. 23 (6): 1021–1039. Bibcode:2004EJMS...23.1021G. doi:10.1016/j.euromechsol.2004.08.006. ISSN 0997-7538.
  22. Gogu, Grigore (2007). "Structural synthesis of fully-isotropic parallel robots with Schönflies motions via theory of linear transformations and evolutionary morphology". European Journal of Mechanics - A/Solids. 26 (2): 242–269. Bibcode:2007EJMS...26..242G. doi:10.1016/j.euromechsol.2006.06.001. ISSN 0997-7538.
  23. "Structural synthesis", Structural Synthesis of Parallel Robots, Solid Mechanics and its Applications, vol. 149, Dordrecht: Springer Netherlands, 2008, pp. 299–328, doi:10.1007/978-1-4020-5710-6_5, ISBN 978-1-4020-5102-9, retrieved 2020-12-14
  24. Gogu, G. (2009). "Structural synthesis of maximally regular T3R2-type parallel robots via theory of linear transformations and evolutionary morphology". Robotica. 27 (1): 79–101. doi:10.1017/s0263574708004542. ISSN 0263-5747. S2CID 32809408.
  25. Wiktor, Peter (2020). "Coupled Cartesian Manipulators". Mechanism and Machine Theory. 161: 103903. doi:10.1016/j.mechmachtheory.2020.103903. ISSN 0094-114X.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.