Catastrophic interference

McCloskey and Cohen (1989) noted the problem of catastrophic interference during two different experiments with backpropagation neural network modelling.

• Experiment 1: Learning the ones and twos addition facts

In their first experiment they trained a standard backpropagation neural network on a single training set consisting of 17 single-digit ones problems (i.e., 1 + 1 through 9 + 1, and 1 + 2 through 1 + 9) until the network could represent and respond properly to all of them. The error between the actual output and the desired output steadily declined across training sessions, which reflected that the network learned to represent the target outputs better across trials. Next, they trained the network on a single training set consisting of 17 single-digit twos problems (i.e., 2 + 1 through 2 + 9, and 1 + 2 through 9 + 2) until the network could represent, respond properly to all of them. They noted that their procedure was similar to how a child would learn their addition facts. Following each learning trial on the twos facts, the network was tested for its knowledge on both the ones and twos addition facts. Like the ones facts, the twos facts were readily learned by the network. However, McCloskey and Cohen noted the network was no longer able to properly answer the ones addition problems even after one learning trial of the twos addition problems. The output pattern produced in response to the ones facts often resembled an output pattern for an incorrect number more closely than the output pattern for a correct number. This is considered to be a drastic amount of error. Furthermore, the problems 2+1 and 2+1, which were included in both training sets, even showed dramatic disruption during the first learning trials of the twos facts.

• Experiment 2: Replication of Barnes and Underwood (1959) study[7]

In their second connectionist model, McCloskey and Cohen attempted to replicate the study on retroactive interference in humans by Barnes and Underwood (1959). They trained the model on A-B and A-C lists and used a context pattern in the input vector (input pattern), to differentiate between the lists. Specifically the network was trained to respond with the right B response when shown the A stimulus and A-B context pattern and to respond with the correct C response when shown the A stimulus and the A-C context pattern. When the model was trained concurrently on the A-B and A-C items then the network readily learned all of the associations correctly. In sequential training the A-B list was trained first, followed by the A-C list. After each presentation of the A-C list, performance was measured for both the A-B and A-C lists. They found that the amount of training on the A-C list in Barnes and Underwood study that lead to 50% correct responses, lead to nearly 0% correct responses by the backpropagation network. Furthermore, they found that the network tended to show responses that looked like the C response pattern when the network was prompted to give the B response pattern. This indicated that the A-C list apparently had overwritten the A-B list. This could be likened to learning the word dog, followed by learning the word stool and then finding that you think of the word stool when presented with the word dog.

McCloskey and Cohen tried to reduce interference through a number of manipulations including changing the number of hidden units, changing the value of the learning rate parameter, overtraining on the A-B list, freezing certain connection weights, changing target values 0 and 1 instead 0.1 and 0.9. However none of these manipulations satisfactorily reduced the catastrophic interference exhibited by the networks.

Overall, McCloskey and Cohen (1989) concluded that:

• at least some interference will occur whenever new learning alters the weights involved representing
• the greater the amount of new learning, the greater the disruption in old knowledge
• interference was catastrophic in the backpropagation networks when learning was sequential but not concurrent

Ratcliff (1990) used multiple sets of backpropagation models applied to standard recognition memory procedures, in which the items were sequentially learned.[2] After inspecting the recognition performance models he found two major problems:

• Well-learned information was catastrophically forgotten as new information was learned in both small and large backpropagation networks.

Even one learning trial with new information resulted in a significant loss of the old information, paralleling the findings of McCloskey and Cohen (1989).[1] Ratcliff also found that the resulting outputs were often a blend of the previous input and the new input. In larger networks, items learned in groups (e.g. AB then CD) were more resistant to forgetting than were items learned singly (e.g. A then B then C...). However, the forgetting for items learned in groups was still large. Adding new hidden units to the network did not reduce interference.

• Discrimination between the studied items and previously unseen items decreased as the network learned more.

This finding contradicts with studies on human memory, which indicated that discrimination increases with learning. Ratcliff attempted to alleviate this problem by adding 'response nodes' that would selectively respond to old and new inputs. However, this method did not work as these response nodes would become active for all inputs. A model which used a context pattern also failed to increase discrimination between new and old items.

Many of the early techniques in reducing representational overlap involved making either the input vectors or the hidden unit activation patterns orthogonal to one another. Lewandowsky and Li (1995)[12] noted that the interference between sequentially learned patterns is minimized if the input vectors are orthogonal to each other. Input vectors are said to be orthogonal to each other if the pairwise product of their elements across the two vectors sum to zero. For example, the patterns [0,0,1,0] and [0,1,0,0] are said to be orthogonal because (0×0 + 0×1 + 1×0 + 0×0) = 0. One of the techniques which can create orthogonal representations at the hidden layers involves bipolar feature coding (i.e., coding using -1 and 1 rather than 0 and 1).[10] Orthogonal patterns tend to produce less interference with each other. However, not all learning problems can be represented using these types of vectors and some studies report that the degree of interference is still problematic with orthogonal vectors.[2]

According to French (1991),[8] catastrophic interference arises in feedforward backpropagation networks due to the interaction of node activations, or activation overlap, that occurs in distributed representations at the hidden layer. Neural networks that employ very localized representations do not show catastrophic interference because of the lack of overlap at the hidden layer. French therefore suggested that reducing the value of activation overlap at the hidden layer would reduce catastrophic interference in distributed networks. Specifically he proposed that this could be done through changing the distributed representations at the hidden layer to 'semi-distributed' representations. A 'semi-distributed' representation has fewer hidden nodes that are active, and/or a lower activation value for these nodes, for each representation, which will make the representations of the different inputs overlap less at the hidden layer. French recommended that this could be done through 'activation sharpening', a technique which slightly increases the activation of a certain number of the most active nodes in the hidden layer, slightly reduces the activation of all the other units and then changes the input-to-hidden layer weights to reflect these activation changes (similar to error backpropagation).

Kortge (1990)[13] proposed a learning rule for training neural networks, called the 'novelty rule', to help alleviate catastrophic interference. As its name suggests, this rule helps the neural network to learn only the components of a new input that differ from an old input. Consequently, the novelty rule changes only the weights that were not previously dedicated to storing information, thereby reducing the overlap in representations at the hidden units. In order to apply the novelty rule, during learning the input pattern is replaced by a novelty vector that represents the components that differ. When the novelty rule is used in a standard backpropagation network there is no, or lessened, forgetting of old items when new items are presented sequentially.[13] However, a limitation is that this rule can only be used with auto-encoder or auto-associative networks, in which the target response for the output layer is identical to the input pattern.

McRae and Hetherington (1993)[9] argued that humans, unlike most neural networks, do not take on new learning tasks with a random set of weights. Rather, people tend to bring a wealth of prior knowledge to a task and this helps to avoid the problem of interference. They showed that when a network is pre-trained on a random sample of data prior to starting a sequential learning task that this prior knowledge will naturally constrain how the new information can be incorporated. This would occur because a random sample of data from a domain that has a high degree of internal structure, such as the English language, training would capture the regularities, or recurring patterns, found within that domain. Since the domain is based on regularities, a newly learned item will tend to be similar to the previously learned information, which will allow the network to incorporate new data with little interference with existing data. Specifically, an input vector that follows the same pattern of regularities as the previously trained data should not cause a drastically different pattern of activation at the hidden layer or drastically alter weights.

Robins (1995)[14] described that catastrophic forgetting can be prevented by rehearsal mechanisms. This means that when new information is added, the neural network is retrained on some of the previously learned information. In general, however, previously learned information may not be available for such retraining. A solution for this is "pseudo-rehearsal", in which the network is not retrained on the actual previous data but on representations of them. Several methods are based upon this general mechanism.

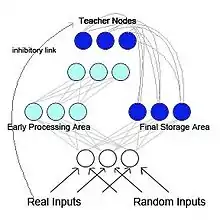
Figure 2: The architecture of a pseudo-recurrent network

French (1997) proposed a pseudo-recurrent backpropagation network (see Figure 2).[5] In this model the network is separated into two functionally distinct but interacting sub-networks. This model is biologically inspired and is based on research from McClelland et al. (1995)[15] McClelland and colleagues suggested that the hippocampus and neocortex act as separable but complementary memory systems, with the hippocampus for short term memory storage and the neocortex for long term memory storage. Information initially stored in the hippocampus can be "transferred" to the neocortex by means of reactivation or replay. In the pseudo-recurrent network, one of the sub-networks acts as an early processing area, akin to the hippocampus, and functions to learn new input patterns. The other sub-network acts as a final-storage area, akin to the neocortex. However, unlike in the McClelland et al. (1995) model, the final-storage area sends internally generated representation back to the early processing area. This creates a recurrent network. French proposed that this interleaving of old representations with new representations is the only way to reduce radical forgetting. Since the brain would most likely not have access to the original input patterns, the patterns that would be fed back to the neocortex would be internally generated representations called pseudo-patterns. These pseudo-patterns are approximations of previous inputs[14] and they can be interleaved with the learning of new inputs.

Inspired by[14] and independently of[5] Ans and Rousset (1997)[16] also proposed a two-network artificial neural architecture with memory self-refreshing that overcomes catastrophic interference when sequential learning tasks are carried out in distributed networks trained by backpropagation. The principle is to learn new external patterns concurrently with internally generated pseudopatterns, or 'pseudo-memories', that reflect the previously learned information. What mainly distinguishes this model from those that use classical pseudorehearsal[14][5] in feedforward multilayer networks is a reverberating process that is used for generating pseudopatterns. After a number of activity re-injections from a single random seed, this process tends to go up to nonlinear network attractors that are more suitable for capturing optimally the deep structure of knowledge distributed within connection weights than the single feedforward pass of activity used in pseudo-rehearsal. The memory self-refreshing procedure turned out to be very efficient in transfer processes[17] and in serial learning of temporal sequences of patterns without catastrophic forgetting.[18]

In recent years, pseudo-rehearsal has re-gained in popularity thanks to the progress in the capabilities of deep generative models. When such deep generative models are used to generate the "pseudo-data" to be rehearsed, this method is typically referred to as generative replay.[19] Such generative replay can effectively prevent catastrophic forgetting, especially when the replay is performed in the hidden layers rather than at the input level.[20][21]

The insights into the mechanisms of memory consolidation during the sleep processes in human and animal brain led to other biologically inspired approaches. While declarative memories are in the classical picture consolidated by hippocampo-neocortical dialog during NREM phase of sleep (see above), some types of procedural memories were suggested not to rely on the hippocampus and involve REM phase of the sleep (e.g.[22], but see[23] for the complexity of the topic). This inspired models where internal representations (memories) created by previous learning are spontaneously replayed during sleep-like periods in the network itself[24][25] (i.e. without help of secondary network performed by generative replay approaches mentioned above).

Latent Learning is a technique used by Gutstein & Stump (2015)[26] to mitigate catastrophic interference by taking advantage of transfer learning. This approach tries to find optimal encodings for any new classes to be learned, so that they are least likely to catastrophically interfere with existing responses. Given a network that has learned to discriminate among one set of classes using Error Correcting Output Codes (ECOC)[27] (as opposed to 1 hot codes), optimal encodings for new classes are chosen by observing the network's average responses to them. Since these average responses arose while learning the original set of classes without any exposure to the new classes, they are referred to as 'Latently Learned Encodings'. This terminology borrows from the concept of Latent Learning, as introduced by Tolman in 1930.[28] In effect, this technique uses transfer learning to avoid catastrophic interference, by making a network's responses to new classes as consistent as possible with existing responses to classes already learned.

Kirkpatrick et al. (2017)[29] proposed elastic weight consolidation (EWC), a method to sequentially train a single artificial neural network on multiple tasks. This technique supposes that some weights of the trained neural network are more important for previously learned tasks than others. During training of the neural network on a new task, changes to the weights of the network are made less likely the greater their importance. To estimate the importance of the network weights, EWC uses probabilistic mechanisms, in particular the Fisher information matrix, but this can be done in other ways as well.[30][31][32]