Cavitation number

The cavitation number (Ca) can be used to predict hydrodynamic cavitation. It has a similar structure as the Euler number, but a different meaning and use:

The cavitation number expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume, and is used to characterize the potential of the flow to cavitate.

It is defined as [1]

Application of the cavitation number to a propeller, a hydrofoil and a constriction.

${\displaystyle \mathrm {Ca} ={\frac {p-p_{\mathrm {v} }}{{\frac {1}{2}}\rho v^{2}}}}$

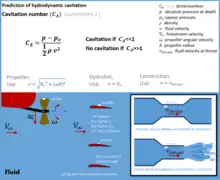
where

• ${\displaystyle \rho }$ is the density of the fluid.
• ${\displaystyle p}$ is the local pressure.
• ${\displaystyle p_{\mathrm {v} }}$ is the vapor pressure of the fluid.
• ${\displaystyle v}$ is a characteristic velocity of the flow.

The cavitation number serves as one of the primary methods for characterizing cavitation within a fluidic system. Low cavitation number indicates a higher probability of cavitation, while high cavitation number indicates no cavitation.

Within a fluid conduit, a pipe or a constraint, as the upstream pressure rises, so does the velocity of the working fluid. However, it's important to note that the increase rate of the square of the velocity greatly surpasses that of the pressure increase. Consequently, the cavitation number exhibits a declining trend with increasing upstream pressure, that is the situation where the system approaches the cavitation.

The inception of cavitation occurs when cavitating bubbles first appear within the system, marking the inception cavitation number. This value represents the highest cavitation number observed within the system in presence of cavitation. Researchers often aim to record cavitation inception at relatively low upstream pressures, particularly when they are pursuing non-destructive applications of this phenomenon.

As the development of cavitating flow progresses, the cavitation number steadily decreases until the system reaches the point of supercavitation, characterized by the highest achievable velocity and flowrate. Lower cavitation numbers are indicative of more intense cavitating flow.

Following supercavitation, the system reaches its fluid-handling limit, even as upstream pressure continues to rise. Consequently, the measured cavitation number embarks on an upward trajectory. This trend is a recurring observation in numerous published articles within the literature.[2]

The Thoma number (${\displaystyle \sigma }$) is a dimensionless quantity that can be used to predict cavitation in the suction of a pump. It is defined as[3]

Application of the Thoma number to a pump for prediction of cavitation

${\displaystyle \mathrm {\sigma } ={\frac {NPSH}{h_{\mathrm {pump} }}}}$

Where ${\displaystyle NPSH}$ is the net positive suction head and ${\displaystyle h_{\mathrm {pump} }}$ is the hydraulic head developed by the pump. The fluid will cavitate in the suction of the pump if the Thoma number is smaller than the critical cavitation parameter or the critical Thoma number defined as

${\displaystyle \mathrm {\sigma _{\mathrm {c} }} ={\frac {NPSHR}{h_{\mathrm {pump} }}}}$

Where ${\displaystyle NPSHR}$ is the net positive suction head required to prevent cavitation. It is a parameter found experimentally for each pump model.

The Garcia-Atance number (${\displaystyle \ G_{A}}$) is a dimensionless quantity that can be used to predict ultrasonic cavitation in a sonicated fluid. It expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the change of pressure due to the acceleration of a column of fluid, and is used to characterize the potential of the sonicated fluid to cavitate. It is defined as[4]

Application of the Garcia-Atance number to predict cavitation produced by an ultrasonic horn.

${\displaystyle \mathrm {G_{A}} ={\frac {p-p_{v}}{\rho aL}}}$

where

• ${\displaystyle \ p}$ is the pressure of the liquid in the absence of acceleration
• ${\displaystyle \ p_{v}}$ is the vapor pressure of the liquid
• ${\displaystyle \rho }$ is the density of the fluid
• ${\displaystyle \ a}$ is the characteristic acceleration of the fluid
• ${\displaystyle \ L}$ is the characteristic length of the liquid or column subjected to acceleration

At low Garcia-Atance numbers (${\displaystyle \ {G_{A}<<1}}$), the fluid tends to cavitate, while at high Garcia-Atance numbers (${\displaystyle \ {G_{A}>>1}}$), the fluid does not cavitate.

In order to apply this number to an ultrasonic horn the acceleration ${\displaystyle \ a}$ is given by:

${\displaystyle a=d(2\pi f)^{2}}$

where ${\displaystyle \ d}$ is the amplitude of the oscillating movement of the horn and ${\displaystyle \ f}$ is the frequency of the oscillating movement of the horn.

While the characteristic length ${\displaystyle \ L}$ should be the smaller of these two:

${\displaystyle L=R}$

or

${\displaystyle L={\frac {c}{2f}}}$

where ${\displaystyle \ R}$ is the radius of the horn, ${\displaystyle \ c}$ is the speed of sound and ${\displaystyle \ f}$ is the frequency of the oscillating movement of the horn. This takes into account that the length of the accelerated fluid column depends on the type of wave front, whether planar or spherical.

The Garcia-Atance number can also be applied for the water hammer cavitation case,[5] where the drop in pressure is due to an acceleration.

• Eurler number for characterising a local pressure drop caused by a restriction in a flow, similar shape to cavitation number