Nutation (botany)

Nutation refers to the bending movements of stems, roots, leaves and other plant organs caused by differences in growth in different parts of the organ. Circumnutation refers specifically to the circular movements often exhibited by the tips of growing plant stems, caused by repeating cycles of differences in growth around the sides of the elongating stem.[1] Nutational movements are usually distinguished from 'variational' movements caused by temporary differences in the water pressure inside plant cells (turgor).

Simple nutation occurs in flat leaves and flower petals, caused by unequal growth of the two sides of the surface. For example, in young leaf buds the outer surface of each leaflet grows faster, causing it to curve over its neighbors and form a compact bud. As the bud expands, growth becomes more rapid on the inner surface of the leaves, causing the bud to open and the leaves to flatten out. Similar inequality of growth, but more sharply localized, leads to the folding and rolling of the leaf in the bud, and to the changing shapes of flower petals.

A circumnutating plant stem

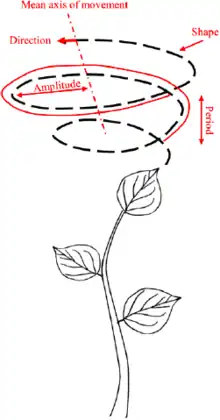
Circumnutational movements are most obvious in growing seedlings, where the combination of circular movement and upward growth causes the tip to move up in a spiral path. The first detailed analysis of circumnutation was Charles Darwin's The Power of Movement in Plants;[2][3] he concluded that most plant movements were modifications of circumnutation, but many counterexamples are now known. Circumnutation is not a direct response to gravity or the direction of illumination, but these factors and many physiological processes can influence its direction, timing and amplitude.[1]

Although the function of circumnutation in most plants is not known, many twining plants have adapted these movements to help them find and twine around vertical objects such as tree trunks, and to help tendrils find and wind around smaller supports.[4][5] The growing tips of the vine or tendril initially swings in wide circles that maximize its chance of bumping into an obstacle (a potential support). Once the obstacle is encountered the circles tighten, causing the vine or tendril to wind around the support as it grows.

The possible theories for plant nutations

Over the last century, studies on plant nutations gave rise to three main theories about their origin:[1][5]

  • The theory of the "internal oscillator", first suggested by Darwin,[2] explains plant nutations as endogenous movements;
  • According to the "gravitropic overshoot" theory,[6][7] nutations in plant shoots might result from delayed gravitropic responses, in the search for the upright pose; this theory was supported theoretically by the existence of a Hopf bifurcation in the so-called sunflower equation;[8]
  • Following experiments in space that showed the persistence of nutations without gravity,[9] some researchers proposed a "two-oscillator" model,[10] accounting for two mechanisms (endogenous oscillations and an exogenous feedback oscillator of gravitropic, proprioceptive or other nature).

New experiments in space showed that the presence of gravity involves and amplifies oscillations of plant shoots, while confirming the occurrence of reduced nutations.[11][12] These findings support the "two-oscillator" hypothesis, which has been revisited to account for the effect of elastic deflections due to gravity loading, previously disregarded.[13] By means of a morphoelastic rod model, some studies showed that a Hopf-like bifurcation phenomenon occurs and elasticity plays an important role in determining the onset of oscillations.[14][15] In particular, the plant shoot might undergo "exogenous" oscillations - which sum to the "endogenous" ones - as it reaches a critical length.[15]

References
  1. Stolarz, Maria (28 October 2014). "Circumnutation as a visible plant action and reaction". Plant Signaling & Behavior. 4 (5): 380–387. doi:10.4161/psb.4.5.8293. PMC 2676747. PMID 19816110. Circumnutation is a helical organ movement widespread among plants.
  2. Darwin, Charles, 1809-1882, author. (2017). The power of movement in plants. ISBN 978-0-19-180518-9. OCLC 981425326. {{cite book}}: |last= has generic name (help)CS1 maint: multiple names: authors list (link)
  3. Brown, Allan H. (September 28, 1992). "Circumnutations: From Darwin to Space Flights" (PDF). Plant Physiology. 101 (2): 345–348. doi:10.1104/pp.101.2.345. PMC 160577. PMID 11537497.
  4. Fiorello, Isabella; Del Dottore, Emanuela; Tramacere, Francesca; Mazzolai, Barbara (2020-03-20). "Taking inspiration from climbing plants: methodologies and benchmarks—a review". Bioinspiration & Biomimetics. 15 (3): 031001. Bibcode:2020BiBi...15c1001F. doi:10.1088/1748-3190/ab7416. ISSN 1748-3190. PMID 32045368.
  5. Mugnai, Sergio; Azzarello, Elisa; Masi, Elisa; Pandolfi, Camilla; Mancuso, Stefano (2015), Mancuso, Stefano; Shabala, Sergey (eds.), "Nutation in Plants", Rhythms in Plants: Dynamic Responses in a Dynamic Environment, Cham: Springer International Publishing, pp. 19–34, doi:10.1007/978-3-319-20517-5_2, ISBN 978-3-319-20517-5, S2CID 197438746, retrieved 2021-03-02
  6. Gradmann, Hans (1927-04-01). "Die Kreisbewegungen der Ranken und der Windepflanzen". Naturwissenschaften (in German). 15 (15): 345–352. Bibcode:1927NW.....15..345G. doi:10.1007/BF01504773. ISSN 1432-1904. S2CID 22480027.
  7. Israelsson, D.; Johnsson, A. (1967). "A Theory for Circumnutations in Helianthus annuus". Physiologia Plantarum. 20 (4): 957–976. doi:10.1111/j.1399-3054.1967.tb08383.x. ISSN 1399-3054.
  8. Somolinos, Alfredo S. (1978). "Periodic solutions of the sunflower equation: 𝑥+(𝑎/𝑟)𝑥+(𝑏/𝑟)sin𝑥(𝑡-𝑟)=0". Quarterly of Applied Mathematics. 35 (4): 465–478. doi:10.1090/qam/465265. ISSN 0033-569X.
  9. "Scopus preview - Scopus - Welcome to Scopus". www.scopus.com. Retrieved 2021-03-02.
  10. "Google Scholar". scholar.google.com. Retrieved 2021-03-02.
  11. Johnsson, A.; Solheim, B. G. B.; Iversen, T.-H. (2009). "Gravity amplifies and microgravity decreases circumnutations in Arabidopsis thaliana stems: results from a space experiment". New Phytologist. 182 (3): 621–629. doi:10.1111/j.1469-8137.2009.02777.x. ISSN 1469-8137. PMID 19320838.
  12. Kobayashi, Akie; Kim, Hye-Jeong; Tomita, Yuta; Miyazawa, Yutaka; Fujii, Nobuharu; Yano, Sachiko; Yamazaki, Chiaki; Kamada, Motoshi; Kasahara, Haruo; Miyabayashi, Sachiko; Shimazu, Toru (2019). "Circumnutational movement in rice coleoptiles involves the gravitropic response: analysis of an agravitropic mutant and space-grown seedlings". Physiologia Plantarum. 165 (3): 464–475. doi:10.1111/ppl.12824. ISSN 1399-3054. PMID 30159898. S2CID 52123435.
  13. Agostinelli, Daniele (2021-03-02). "The mystery of plant nutations: Is mathematics of any help?". Medium. Retrieved 2021-03-02.
  14. Agostinelli, Daniele; Lucantonio, Alessandro; Noselli, Giovanni; DeSimone, Antonio (March 2020). "Nutations in growing plant shoots: The role of elastic deformations due to gravity loading". Journal of the Mechanics and Physics of Solids. 136: 103702. Bibcode:2020JMPSo.13603702A. doi:10.1016/j.jmps.2019.103702.
  15. Agostinelli, Daniele; DeSimone, Antonio; Noselli, Giovanni (2021). "Nutations in plant shoots: Endogenous and exogenous factors in the presence of mechanical deformations". Frontiers in Plant Science. 12: 608005. doi:10.3389/fpls.2021.608005. ISSN 1664-462X. PMC 8023405. PMID 33833768.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.