Clique-width

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :

  1. Creation of a new vertex v with label i (denoted by i(v))
  2. Disjoint union of two labeled graphs G and H (denoted by )
  3. Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
  4. Renaming label i to label j (denoted by ρ(i,j))
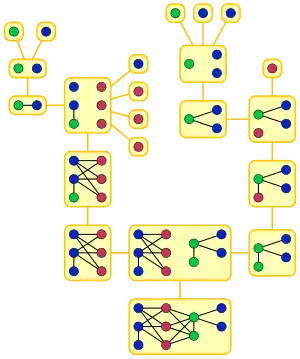
Construction of a distance-hereditary graph of clique-width 3 by disjoint unions, relabelings, and label-joins. Vertex labels are shown as colors.

Graphs of bounded clique-width include the cographs and distance-hereditary graphs. Although it is NP-hard to compute the clique-width when it is unbounded, and unknown whether it can be computed in polynomial time when it is bounded, efficient approximation algorithms for clique-width are known. Based on these algorithms and on Courcelle's theorem, many graph optimization problems that are NP-hard for arbitrary graphs can be solved or approximated quickly on the graphs of bounded clique-width.

The construction sequences underlying the concept of clique-width were formulated by Courcelle, Engelfriet, and Rozenberg in 1990[1] and by Wanke (1994). The name "clique-width" was used for a different concept by Chlebíková (1992). By 1993, the term already had its present meaning.[2]

Special classes of graphs

Cographs are exactly the graphs with clique-width at most 2.[3] Every distance-hereditary graph has clique-width at most 3. However, the clique-width of unit interval graphs is unbounded (based on their grid structure).[4] Similarly, the clique-width of bipartite permutation graphs is unbounded (based on similar grid structure).[5] Based on the characterization of cographs as the graphs with no induced subgraph isomorphic to a path with four vertices, the clique-width of many graph classes defined by forbidden induced subgraphs has been classified.[6]

Other graphs with bounded clique-width include the k-leaf powers for bounded values of k; these are the induced subgraphs of the leaves of a tree T in the graph power Tk. However, leaf powers with unbounded exponents do not have bounded clique-width.[7]

Bounds

Courcelle & Olariu (2000) and Corneil & Rotics (2005) proved the following bounds on the clique-width of certain graphs:

  • If a graph has clique-width at most k, then so does every induced subgraph of the graph.[8]
  • The complement graph of a graph of clique-width k has clique-width at most 2k.[9]
  • The graphs of treewidth w have clique-width at most 3 · 2w − 1. The exponential dependence in this bound is necessary: there exist graphs whose clique-width is exponentially larger than their treewidth.[10] In the other direction, graphs of bounded clique-width can have unbounded treewidth; for instance, n-vertex complete graphs have clique-width 2 but treewidth n − 1. However, graphs of clique-width k that have no complete bipartite graph Kt,t as a subgraph have treewidth at most 3k(t − 1) − 1. Therefore, for every family of sparse graphs, having bounded treewidth is equivalent to having bounded clique-width.[11]
  • Another graph parameter, the rank-width, is bounded in both directions by the clique-width: rank-width ≤ clique-width ≤ 2rank-width + 1.[12]

Additionally, if a graph G has clique-width k, then the graph power Gc has clique-width at most 2kck.[13] Although there is an exponential gap in both the bound for clique-width from treewidth and the bound for clique-width of graph powers, these bounds do not compound each other: if a graph G has treewidth w, then Gc has clique-width at most 2(c + 1)w + 1 − 2, only singly exponential in the treewidth.[14]

Computational complexity
Unsolved problem in mathematics:

Can graphs of bounded clique-width be recognized in polynomial time?

(more unsolved problems in mathematics)

Many optimization problems that are NP-hard for more general classes of graphs may be solved efficiently by dynamic programming on graphs of bounded clique-width, when a construction sequence for these graphs is known.[15][16] In particular, every graph property that can be expressed in MSO1 monadic second-order logic (a form of logic allowing quantification over sets of vertices) has a linear-time algorithm for graphs of bounded clique-width, by a form of Courcelle's theorem.[16]

It is also possible to find optimal graph colorings or Hamiltonian cycles for graphs of bounded clique-width in polynomial time, when a construction sequence is known, but the exponent of the polynomial increases with the clique-width, and evidence from computational complexity theory shows that this dependence is likely to be necessary.[17] The graphs of bounded clique-width are χ-bounded, meaning that their chromatic number is at most a function of the size of their largest clique.[18]

The graphs of clique-width three can be recognized, and a construction sequence found for them, in polynomial time using an algorithm based on split decomposition.[19] For graphs of unbounded clique-width, it is NP-hard to compute the clique-width exactly, and also NP-hard to obtain an approximation with sublinear additive error.[20] However, when the clique-width is bounded, it is possible to obtain a construction sequence of bounded width (exponentially larger than the actual clique-width) in polynomial time,[21] in particular in quadratic time in the number of vertices.[22] It remains open whether the exact clique-width, or a tighter approximation to it, can be calculated in fixed-parameter tractable time, whether it can be calculated in polynomial time for every fixed bound on the clique-width, or even whether the graphs of clique-width four can be recognized in polynomial time.[20]

The theory of graphs of bounded clique-width resembles that for graphs of bounded treewidth, but unlike treewidth allows for dense graphs. If a family of graphs has bounded clique-width, then either it has bounded treewidth or every complete bipartite graph is a subgraph of a graph in the family.[11] Treewidth and clique-width are also connected through the theory of line graphs: a family of graphs has bounded treewidth if and only if their line graphs have bounded clique-width.[23]

The graphs of bounded clique-width also have bounded twin-width.[24]

Notes
  1. Courcelle, Engelfriet & Rozenberg (1993).
  2. Courcelle (1993).
  3. Courcelle & Olariu (2000).
  4. Golumbic & Rotics (2000).
  5. Brandstädt & Lozin (2003).
  6. Brandstädt et al. (2005); Brandstädt et al. (2006).
  7. Brandstädt & Hundt (2008); Gurski & Wanke (2009).
  8. Courcelle & Olariu (2000), Corollary 3.3.
  9. Courcelle & Olariu (2000), Theorem 4.1.
  10. Corneil & Rotics (2005), strengthening Courcelle & Olariu (2000), Theorem 5.5.
  11. Gurski & Wanke (2000).
  12. Oum & Seymour (2006).
  13. Todinca (2003).
  14. Gurski & Wanke (2009).
  15. Cogis & Thierry (2005).
  16. Courcelle, Makowsky & Rotics (2000).
  17. Fomin et al. (2010).
  18. Dvořák & Král' (2012).
  19. Corneil et al. (2012).
  20. Fellows et al. (2009).
  21. Oum & Seymour (2006); Hliněný & Oum (2008); Oum (2008); Fomin & Korhonen (2022).
  22. Fomin & Korhonen (2022).
  23. Gurski & Wanke (2007).
  24. Bonnet et al. (2022).

References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.