Clustered planarity

In graph drawing, a clustered planar graph is a graph together with a hierarchical clustering on its vertices, such that the graph can be drawn together with a collection of simple closed curves surrounding each cluster with no crossings between graph edges or clusters.[1]

A clustered planar drawing

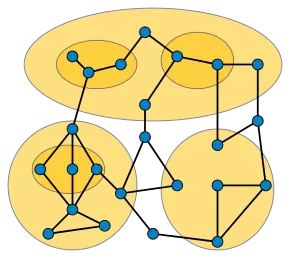
The clustering can be described combinatorially by a collection of subsets of the vertices such that, for each two subsets, either both are disjoint or one is contained in the other. It is not required that the clustering be maximal nor that every vertex belong to a cluster. In a clustered planar drawing, no two edges may cross each other (that is, the graph must be planar), no two of the curves representing clusters may cross each other, an edge may cross a cluster boundary only if it connects a vertex inside the cluster to a vertex outside the cluster, and when an edge and cluster boundary cross they may cross only once.[1] After much past work on the problem, a polynomial-time algorithm testing clustered planarity was found in 2019 by Radoslav Fulek and Csaba Tóth.[2]