Compton generator
A Compton generator[1][2] or Compton tube[3] is an apparatus for experiment to demonstrate the Earth's rotation, similar to the Foucault pendulum and to gyroscope devices.[4] Arthur Compton (Nobel Prize in Physics in 1927) published it during his fourth year at the College of Wooster in 1913.[5]

Explanation of apparatus
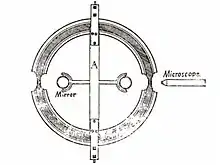
A Compton generator is a circular hollow glass ring tube shaped like a doughnut, the inside of which is filled with water.[1] If the ring lies flat on the table, the water in the ring is stationary, and it is then turned over by rotating itself 180 degree around a diameter, such that it again lies flat on the table surface, which is horizontal. The result of the experiment is that the water moves with a certain constant drift velocity around the tube after the doughnut has been rotated. If there were no friction with the walls, the water would continue to circulate indefinitely.[1]
The ring used in the initial experiment was made of one inch brass tubing bent into a circle eighteen inches in diameter, where the windows were placed the tube was constricted to a diameter of about 3/8 inches (9.5 mm).[6]
Compton used small droplets of coal oil mixed in the water to measure the drift velocity under a microscope.[7]
Analysis
Assume the diameter of the glass tube is much smaller than the diameter of the ring, and is the radius of the ring, is the Earth rotation rate and is the latitude.
Initially the ring is horizontal and the water is stationary. Second the ring is then quickly rotated by 180° around its East-West diameter and stopped, such that it again lies flat on the table surface, which is horizontal. At this time, the velocity of the water in the tube is given by
Note that a rotation from the vertical to the vertical position produces the velocity of the water in the tube is given by
This is derived by first integrating the torque due to the Coriolis force around the ring, then integrating the torque over the time it takes for the ring to flip, to obtain the change in angular momentum.[4]
With these two equations, one can solve for both , thus finding both the rotation speed of earth and the latitude of the apparatus.
Experimental verification
Compton used this measured drift velocity to determine his latitude to within 3% accuracy.[7] He also used it to measure the rotational period of earth to an accuracy of 16 minutes per day (accuracy of 1%). By careful methods he could observe the effect in a ring with a radius of only 9 inches (23 cm).[8]
Earth's rotation is 7.3 × 10−5 radians/second. In the original report, Compton used a ring of 1 meter in radius at the College of Wooster (latitude 41 degrees). This would translate to a velocity of about .
References
- Analytical Mechanics, p. 280.
- Classical Mechanics, p. 365.
- Blackie's Dictionary of Physics, p. 72.
- A laboratory method of demonstrating the Earth's rotation 1913, p. 803.
- Karukstis, Kerry K. (2020-12-01). "Analysis of the Undergraduate Research Movement: Origins, Developments, and Current Challenges". Council on Undergraduate Research Quarterly. 3 (2): 46–55. doi:10.18833/spur/3/2/8.
- A determination of latitude, Azimuth, and the length of the day independent of astronomical observations 1915, p. 110&111.
- Analytical Mechanics, p. 281.
- McKinney, William M. (April 1962). "Experimental Proofs of the Earth's Rotation". Journal of Geography. 61 (4): 171–174. doi:10.1080/00221346208982136. ISSN 0022-1341.
Bibliography
Journal
- Compton, Arthur Holly (1913). "A laboratory method of demonstrating the Earth's rotation". Science. 37 (960): 803–806. Bibcode:1913Sci....37..803C. doi:10.1126/science.37.960.803. PMID 17838837.
- Compton, Arthur Holly (1915). "A determination of latitude, Azimuth, and the length of the day independent of astronomical observations". Physical Review. 5 (2): 109–117. Bibcode:1915PhRv....5..109C. doi:10.1103/PhysRev.5.109.
- Compton, Arthur Holly (1915). "Watching the Earth revolve". Scientific American Supplement. 79 (2047supp): 196–197. doi:10.1038/scientificamerican03271915-196supp.
Books
- Hand, Louis N. (1999). Analytical Mechanics. Cambridge University Press. ISBN 978-0521575720.
- Taylor, John R. (2005). Classical Mechanics. S.Chand & Company Ltd. ISBN 978-1891389221.
- Blackie's Dictionary of Physics. S.Chand & Company Ltd. 2000. ISBN 978-8121942379.