Conical spiral
In mathematics, a conical spiral, also known as a conical helix,[1] is a space curve on a right circular cone, whose floor projection is a plane spiral. If the floor projection is a logarithmic spiral, it is called conchospiral (from conch).



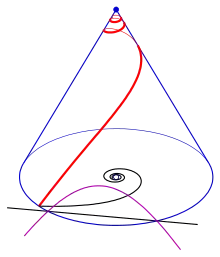
Parametric representation
In the --plane a spiral with parametric representation
a third coordinate can be added such that the space curve lies on the cone with equation :
Such curves are called conical spirals.[2] They were known to Pappos.
Parameter is the slope of the cone's lines with respect to the --plane.
A conical spiral can instead be seen as the orthogonal projection of the floor plan spiral onto the cone.
Examples
- 1) Starting with an archimedean spiral gives the conical spiral (see diagram)
- In this case the conical spiral can be seen as the intersection curve of the cone with a helicoid.
- 2) The second diagram shows a conical spiral with a Fermat's spiral as floor plan.
- 3) The third example has a logarithmic spiral as floor plan. Its special feature is its constant slope (see below).
- Introducing the abbreviation gives the description: .
- 4) Example 4 is based on a hyperbolic spiral . Such a spiral has an asymptote (black line), which is the floor plan of a hyperbola (purple). The conical spiral approaches the hyperbola for .
Properties
The following investigation deals with conical spirals of the form and , respectively.
Slope
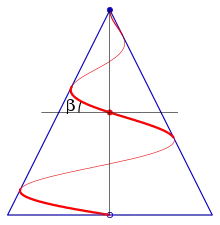
The slope at a point of a conical spiral is the slope of this point's tangent with respect to the --plane. The corresponding angle is its slope angle (see diagram):
A spiral with gives:
For an archimedean spiral is and hence its slope is
- For a logarithmic spiral with the slope is ( ).
Because of this property a conchospiral is called an equiangular conical spiral.
Arclength
The length of an arc of a conical spiral can be determined by
For an archimedean spiral the integral can be solved with help of a table of integrals, analogously to the planar case:
For a logarithmic spiral the integral can be solved easily:
In other cases elliptical integrals occur.
Development
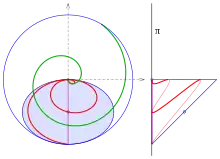
For the development of a conical spiral[3] the distance of a curve point to the cone's apex and the relation between the angle and the corresponding angle of the development have to be determined:
Hence the polar representation of the developed conical spiral is:
In case of the polar representation of the developed curve is
which describes a spiral of the same type.
- If the floor plan of a conical spiral is an archimedean spiral than its development is an archimedean spiral.
- In case of a hyperbolic spiral () the development is congruent to the floor plan spiral.
In case of a logarithmic spiral the development is a logarithmic spiral:
Tangent trace
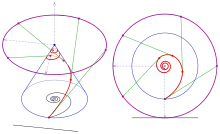
The collection of intersection points of the tangents of a conical spiral with the --plane (plane through the cone's apex) is called its tangent trace.
For the conical spiral
the tangent vector is
and the tangent:
The intersection point with the --plane has parameter and the intersection point is
gives and the tangent trace is a spiral. In the case (hyperbolic spiral) the tangent trace degenerates to a circle with radius (see diagram). For one has and the tangent trace is a logarithmic spiral, which is congruent to the floor plan, because of the self-similarity of a logarithmic spiral.

References
- "Conical helix". MATHCURVE.COM. Retrieved 2022-03-03.
- Siegmund Günther, Anton Edler von Braunmühl, Heinrich Wieleitner: Geschichte der mathematik. G. J. Göschen, 1921, p. 92.
- Theodor Schmid: Darstellende Geometrie. Band 2, Vereinigung wissenschaftlichen Verleger, 1921, p. 229.