Rado graph

Ackermann (1937) and Rado (1964) constructed the Rado graph using the BIT predicate as follows. They identified the vertices of the graph with the natural numbers 0, 1, 2, ... An edge connects vertices ${\displaystyle x}$ and ${\displaystyle y}$ in the graph (where ${\displaystyle x<y}$) whenever the ${\displaystyle x}$th bit of the binary representation of ${\displaystyle y}$ is nonzero. Thus, for instance, the neighbors of vertex 0 consist of all odd-numbered vertices, because the numbers whose 0th bit is nonzero are exactly the odd numbers. Vertex 1 has one smaller neighbor, vertex 0, as 1 is odd and vertex 0 is connected to all odd vertices. The larger neighbors of vertex 1 are all vertices with numbers congruent to 2 or 3 modulo 4, because those are exactly the numbers with a nonzero bit at index 1.[1]

The Rado graph arises almost surely in the Erdős–Rényi model of a random graph on countably many vertices. Specifically, one may form an infinite graph by choosing, independently and with probability 1/2 for each pair of vertices, whether to connect the two vertices by an edge. With probability 1 the resulting graph is isomorphic to the Rado graph. This construction also works if any fixed probability ${\displaystyle p}$ not equal to 0 or 1 is used in place of 1/2.[2]

This result, shown by Paul Erdős and Alfréd Rényi (1963), justifies the definite article in the common alternative name "the random graph" for the Rado graph. Repeatedly drawing a finite graph from the Erdős–Rényi model will in general lead to different graphs; however, when applied to a countably infinite graph, the model almost always produces the same infinite graph.[3]

For any graph generated randomly in this way, the complement graph can be obtained at the same time by reversing all the choices: including an edge when the first graph did not include the same edge, and vice versa. This construction of the complement graph is an instance of the same process of choosing randomly and independently whether to include each edge, so it also (with probability 1) generates the Rado graph. Therefore, the Rado graph is a self-complementary graph.[4]

In one of Ackermann's original 1937 constructions, the vertices of the Rado graph are indexed by the hereditarily finite sets, and there is an edge between two vertices exactly when one of the corresponding finite sets is a member of the other. A similar construction can be based on Skolem's paradox, the fact that there exists a countable model for the first-order theory of sets. One can construct the Rado graph from such a model by creating a vertex for each set, with an edge connecting each pair of sets where one set in the pair is a member of the other.[5]

The Rado graph may also be formed by a construction resembling that for Paley graphs, taking as the vertices of a graph all the prime numbers that are congruent to 1 modulo 4, and connecting two vertices by an edge whenever one of the two numbers is a quadratic residue modulo the other. By quadratic reciprocity and the restriction of the vertices to primes congruent to 1 mod 4, this is a symmetric relation, so it defines an undirected graph, which turns out to be isomorphic to the Rado graph.[6]

Another construction of the Rado graph shows that it is an infinite circulant graph, with the integers as its vertices and with an edge between each two integers whose distance (the absolute value of their difference) belongs to a particular set ${\displaystyle S}$. To construct the Rado graph in this way, ${\displaystyle S}$ may be chosen randomly, or by choosing the indicator function of ${\displaystyle S}$ to be the concatenation of all finite binary sequences.[7]

The Rado graph can also be constructed as the block intersection graph of an infinite block design in which the number of points and the size of each block are countably infinite.[8] It can also be constructed as the Fraïssé limit of the class of finite graphs.[9]

The extension property of the Rado graph: for every two disjoint finite sets of vertices ${\displaystyle U}$ and ${\displaystyle V}$, there exists another vertex ${\displaystyle x}$ connected to everything in ${\displaystyle U}$, and to nothing in ${\displaystyle V}$

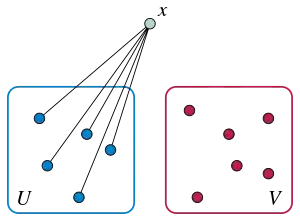
The Rado graph satisfies the following extension property: for every two disjoint finite sets of vertices ${\displaystyle U}$ and ${\displaystyle V}$, there exists a vertex ${\displaystyle x}$ outside both sets that is connected to all vertices in ${\displaystyle U}$, but has no neighbors in ${\displaystyle V}$.[2] For instance, with the binary-number definition of the Rado graph, let

$${\displaystyle x=2^{1+\max(U\cup V)}+\sum _{u\in U}2^{u}.}$$

Then the nonzero bits in the binary representation of ${\displaystyle x}$ cause it to be adjacent to everything in ${\displaystyle U}$. However, ${\displaystyle x}$ has no nonzero bits in its binary representation corresponding to vertices in ${\displaystyle V}$, and ${\displaystyle x}$ is so large that the ${\displaystyle x}$th bit of every element of ${\displaystyle V}$ is zero. Thus, ${\displaystyle x}$ is not adjacent to any vertex in ${\displaystyle V}$.[10]

With the random-graph definition of the Rado graph, each vertex outside the union of ${\displaystyle U}$ and ${\displaystyle V}$ has probability ${\displaystyle 1/2^{|U|+|V|}}$ of fulfilling the extension property, independently of the other vertices. Because there are infinitely many vertices to choose from, each with the same finite probability of success, the probability is one that there exists a vertex that fulfils the extension property.[2] With the Paley graph definition, for any sets ${\displaystyle U}$ and ${\displaystyle V}$, by the Chinese remainder theorem, the numbers that are quadratic residues modulo every prime in ${\displaystyle U}$ and nonresidues modulo every prime in ${\displaystyle V}$ form a periodic sequence, so by Dirichlet's theorem on primes in arithmetic progressions this number-theoretic graph has the extension property.[6]

The extension property can be used to build up isomorphic copies of any finite or countably infinite graph ${\displaystyle G}$ within the Rado graph, as induced subgraphs. To do so, order the vertices of ${\displaystyle G}$, and add vertices in the same order to a partial copy of ${\displaystyle G}$ within the Rado graph. At each step, the next vertex in ${\displaystyle G}$ will be adjacent to some set ${\displaystyle U}$ of vertices in ${\displaystyle G}$ that are earlier in the ordering of the vertices, and non-adjacent to the remaining set ${\displaystyle V}$ of earlier vertices in ${\displaystyle G}$. By the extension property, the Rado graph will also have a vertex ${\displaystyle x}$ that is adjacent to all the vertices in the partial copy that correspond to members of ${\displaystyle U}$, and non-adjacent to all the vertices in the partial copy that correspond to members of ${\displaystyle V}$. Adding ${\displaystyle x}$ to the partial copy of ${\displaystyle G}$ produces a larger partial copy, with one more vertex.[11]

This method forms the basis for a proof by induction, with the 0-vertex subgraph as its base case, that every finite or countably infinite graph is an induced subgraph of the Rado graph.[11]

The Rado graph is, up to graph isomorphism, the only countable graph with the extension property. For example, let ${\displaystyle G}$ and ${\displaystyle H}$ be two countable graphs with the extension property, let ${\displaystyle G_{i}}$ and ${\displaystyle H_{i}}$ be isomorphic finite induced subgraphs of ${\displaystyle G}$ and ${\displaystyle H}$ respectively, and let ${\displaystyle g_{i}}$ and ${\displaystyle h_{i}}$ be the first vertices in an enumeration of the vertices of ${\displaystyle G}$ and ${\displaystyle H}$ respectively that do not belong to ${\displaystyle G_{i}}$ and ${\displaystyle H_{i}}$. Then, by applying the extension property twice, one can find isomorphic induced subgraphs ${\displaystyle G_{i+1}}$ and ${\displaystyle H_{i+1}}$ that include ${\displaystyle g_{i}}$ and ${\displaystyle h_{i}}$ together with all the vertices of the previous subgraphs. By repeating this process, one may build up a sequence of isomorphisms between induced subgraphs that eventually includes every vertex in ${\displaystyle G}$ and ${\displaystyle H}$. Thus, by the back-and-forth method, ${\displaystyle G}$ and ${\displaystyle H}$ must be isomorphic.[12] Because the graphs constructed by the random graph construction, binary number construction, and Paley graph construction are all countable graphs with the extension property, this argument shows that they are all isomorphic to each other.[13]

Applying the back-and-forth construction to any two isomorphic finite subgraphs of the Rado graph extends their isomorphism to an automorphism of the entire Rado graph. The fact that every isomorphism of finite subgraphs extends to an automorphism of the whole graph is expressed by saying that the Rado graph is ultrahomogeneous. In particular, there is an automorphism taking any ordered pair of adjacent vertices to any other such ordered pair, so the Rado graph is a symmetric graph.[12]

The automorphism group of the Rado graph is a simple group, whose number of elements is the cardinality of the continuum. Every subgroup of this group whose index is less than the cardinality of the continuum contains the pointwise stabilizer of a finite set of vertices, and furthermore is contained within the setwise stabilizer of the same set.[14] The statement about pointwise stabilizers is called the small index property,[14] and proving it required showing that for every finite graph ${\displaystyle X}$, there is a finite graph ${\displaystyle Z}$ containing ${\displaystyle X}$ as an induced subgraph such that every isomorphism between induced subgraphs of ${\displaystyle X}$ extends to an automorphism of ${\displaystyle Z}$.[15] This is called the extension property for partial automorphisms and has since been generalized to further structures in order to show the small index property and other properties.[16]

The construction of the Rado graph as an infinite circulant graph shows that its symmetry group includes automorphisms that generate a transitive infinite cyclic group. The difference set of this construction (the set of distances in the integers between adjacent vertices) can be constrained to include the difference 1, without affecting the correctness of this construction, from which it follows that the Rado graph contains an infinite Hamiltonian path whose symmetries are a subgroup of the symmetries of the whole graph.[17]

If a graph ${\displaystyle G}$ is formed from the Rado graph by deleting any finite number of edges or vertices, or adding a finite number of edges, the change does not affect the extension property of the graph. For any pair of sets ${\displaystyle U}$ and ${\displaystyle V}$ it is still possible to find a vertex in the modified graph that is adjacent to everything in ${\displaystyle U}$ and nonadjacent to everything in ${\displaystyle V}$, by adding the modified parts of ${\displaystyle G}$ to ${\displaystyle V}$ and applying the extension property in the unmodified Rado graph. Therefore, any finite modification of this type results in a graph that is isomorphic to the Rado graph.[18]

For any partition of the vertices of the Rado graph into two sets ${\displaystyle A}$ and ${\displaystyle B}$, or more generally for any partition into finitely many subsets, at least one of the subgraphs induced by one of the partition sets is isomorphic to the whole Rado graph. Cameron (2001) gives the following short proof: if none of the parts induces a subgraph isomorphic to the Rado graph, they all fail to have the extension property, and one can find pairs of sets ${\displaystyle U_{i}}$ and ${\displaystyle V_{i}}$ that cannot be extended within each subgraph. But then, the union of the sets ${\displaystyle U_{i}}$ and the union of the sets ${\displaystyle V_{i}}$ would form a set that could not be extended in the whole graph, contradicting the Rado graph's extension property. This property of being isomorphic to one of the induced subgraphs of any partition is held by only three countably infinite undirected graphs: the Rado graph, the complete graph, and the empty graph.[19] Bonato, Cameron & Delić (2000) and Diestel et al. (2007) investigate infinite directed graphs with the same partition property; all are formed by choosing orientations for the edges of the complete graph or the Rado graph.

A related result concerns edge partitions instead of vertex partitions: for every partition of the edges of the Rado graph into finitely many sets, there is a subgraph isomorphic to the whole Rado graph that uses at most two of the colors. However, there may not necessarily exist an isomorphic subgraph that uses only one color of edges.[20] More generally, for every finite graph ${\displaystyle A}$ there is a number ${\displaystyle d_{A}}$ (called the big Ramsey degree of ${\displaystyle A}$ in the Rado graph) such that for every partition of the copies of ${\displaystyle A}$ in the Rado graph into finitely many sets, there is an induced subgraph isomorphic to the whole Rado graph that uses at most ${\displaystyle d_{A}}$ of the colors.[21][22]

The first-order language of graphs is the collection of well-formed sentences in mathematical logic formed from variables representing the vertices of graphs, universal and existential quantifiers, logical connectives, and predicates for equality and adjacency of vertices. For instance, the condition that a graph does not have any isolated vertices may be expressed by the sentence

$${\displaystyle \forall u:\exists v:u\sim v}$$

where the ${\displaystyle \sim }$ symbol indicates the adjacency relation between two vertices.[23] This sentence ${\displaystyle S}$ is true for some graphs, and false for others; a graph ${\displaystyle G}$ is said to model ${\displaystyle S}$, written ${\displaystyle G\models S}$, if ${\displaystyle S}$ is true of the vertices and adjacency relation of ${\displaystyle G}$.[24]

The extension property of the Rado graph may be expressed by a collection of first-order sentences ${\displaystyle E_{i,j}}$, stating that for every choice of ${\displaystyle i}$ vertices in a set ${\displaystyle A}$ and ${\displaystyle j}$ vertices in a set ${\displaystyle B}$, all distinct, there exists a vertex adjacent to everything in ${\displaystyle A}$ and nonadjacent to everything in ${\displaystyle B}$.[25] For instance, ${\displaystyle E_{1,1}}$ can be written as

$${\displaystyle \forall a:\forall b:a\neq b\rightarrow \exists c:c\neq a\wedge c\neq b\wedge c\sim a\wedge \lnot (c\sim b).}$$

Gaifman (1964) proved that the sentences ${\displaystyle E_{i,j}}$, together with additional sentences stating that the adjacency relation is symmetric and antireflexive (that is, that a graph modeling these sentences is undirected and has no self-loops), are the axioms of a complete theory. This means that, for each first-order sentence ${\displaystyle S}$, exactly one of ${\displaystyle S}$ and its negation can be proven from these axioms. Because the Rado graph models the extension axioms, it models all sentences in this theory.[26]

In logic, a theory that has only one model (up to isomorphism) with a given infinite cardinality ${\displaystyle \lambda }$ is called ${\displaystyle \lambda }$-categorical. The fact that the Rado graph is the unique countable graph with the extension property implies that it is also the unique countable model for its theory. This uniqueness property of the Rado graph can be expressed by saying that the theory of the Rado graph is ω-categorical. Łoś and Vaught proved in 1954 that when a theory is ${\displaystyle \lambda }$–categorical (for some infinite cardinal ${\displaystyle \lambda }$) and, in addition, has no finite models, then the theory must be complete.[27] Therefore, Gaifman's theorem that the theory of the Rado graph is complete follows from the uniqueness of the Rado graph by the Łoś–Vaught test.[28]

As Fagin (1976) proved, the first-order sentences provable from the extension axioms and modeled by the Rado graph are exactly the sentences true for almost all random finite graphs. This means that if one chooses an ${\displaystyle n}$-vertex graph uniformly at random among all graphs on ${\displaystyle n}$ labeled vertices, then the probability that such a sentence will be true for the chosen graph approaches one in the limit as ${\displaystyle n}$ approaches infinity. Symmetrically, the sentences that are not modeled by the Rado graph are false for almost all random finite graphs. It follows that every first-order sentence is either almost always true or almost always false for random finite graphs, and these two possibilities can be distinguished by determining whether the Rado graph models the sentence. Fagin's proof uses the compactness theorem.[29] Based on this equivalence, the theory of sentences modeled by the Rado graph has been called "the theory of the random graph" or "the almost sure theory of graphs".

Because of this 0-1 law, it is possible to test whether any particular first-order sentence is modeled by the Rado graph in a finite amount of time, by choosing a large enough value of ${\displaystyle n}$ and counting the number of ${\displaystyle n}$-vertex graphs that model the sentence. However, here, "large enough" is at least exponential in the size of the sentence. For instance the extension axiom ${\displaystyle E_{k,0}}$ implies the existence of a ${\displaystyle (k+1)}$-vertex clique, but a clique of that size exists with high probability only in random graphs of size exponential in ${\displaystyle k}$. It is unlikely that determining whether the Rado graph models a given sentence can be done more quickly than exponential time, as the problem is PSPACE-complete.[30]

The Rado graph is ultrahomogeneous, and thus is the Fraïssé limit of its class of finite substructures, i.e. the class of finite graphs.[31] Given that it is also in a finite relational language, ultrahomogeneity is equivalent to its theory having quantifier elimination and being ω-categorical.[32] As the Rado graph is thus the countable model of a countable ω-categorical theory, it is both prime and saturated.[33][34]

The theory of the Rado graph is a prototypical example of a theory with the independence property, and of a simple theory that is not stable.[35]