Critical path drag

Critical path drag is a project management metric[1] developed by Stephen Devaux as part of the Total Project Control (TPC) approach to schedule analysis and compression [2] in the critical path method of scheduling. Critical path drag is the amount of time that an activity or constraint on the critical path is adding to the project duration. Alternatively, it is the maximum amount of time that one can shorten the activity before it is no longer on the critical path or before its duration becomes zero.

In networks where all dependencies are finish-to-start (FS) relationships (i.e., where a predecessor must finish before a successor starts), the drag of a critical path activity is equal to whichever is less: its remaining duration or (if there is one or more parallel activity) the total float of the parallel activity that has the least total float.[3]

Activity-on-node diagram showing critical path schedule, along with total float and critical path drag computations

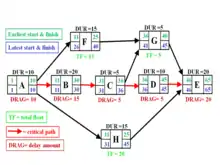
In this diagram, Activities A, B, C, D, and E comprise the critical path, while Activities F, G, and H are off the critical path with floats of 15 days, 5 days, and 20 days respectively. (Note that the Early and Late Finish of Task C should be 35 and not 36). Whereas activities that are off the critical path have float and are therefore not delaying completion of the project, those on the critical path have critical path drag, i.e., they delay project completion.

1. Activities A and E have nothing in parallel and therefore have drags of 10 days and 20 days respectively.
2. Activities B and C are both parallel to F (float of 15) and H (float of 20). B has a duration of 20 and drag of 15 (equal to F's float), while C has a duration of only 5 days and thus drag of only 5.
3. Activity D, with a duration of 10 days, is parallel to G (float of 5) and H (float of 20) and therefore its drag is equal to 5, the float of G.

In network schedules that include start-to-start (SS), finish-to-finish (FF) and start-to-finish (SF) relationships and lags, drag computation can be quite complex, often requiring either the decomposition of critical path activities into their components so as to create all relationships as finish-to-start, or the use of scheduling software that computes critical path drag with complex dependencies.

A quick way to compute the drag of a critical path activity that has one or more start-to-start or start-to-start plus lag successors is that the drag of the critical path activity that has such successors will be equal to whichever is less: the duration of the predecessor activity OR the sum of the lag plus total float of whichever SS successor has the LEAST lag plus total float. This is shown in the diagram where Activity A has four SS+lag successors: B, C, E, and F. The drag-plus-lag of B is 3 + 12 = 15. For each of C, E, and F, it is 20, 12, and 10 respectively. The lowest is F with 10. Since Activity A's duration is 20 which is higher than F's drag-plus-lag of 10, A's drag is 10. In other words, A is adding 10 units of time to the project duration. (If there were another separate parallel path, not in this diagram, that had float of 9 or fewer units, then A's drag would be equal to that float amount as it would be less than 10.)

Activity-on-node diagram showing critical path drag computation for an activity with start-to-start successors

Note that in the SS + lag relationship, the drag is in the work scheduled in the predecessor activity, e.g., digging the first 100 metres of trench in order to start laying the pipe. If the volume of work in the first part of the activity can be performed faster, the lag to the trench-digging can shrink, decreasing the drag in the predecessor and compressing the critical path. Occasionally, however, the lag on an SS relationship may be strictly a "time lag" representing a waiting period rather than work in the predecessor. In that case, the drag should be associated with the lag as that constraint is the delaying factor that must be addressed to shorten the project. Time lags are far more common on finish-to-start and finish-to-finish relationships ("Wait for cement to dry") than on SS relationships.

Critical path drag is often combined with an estimate of the increased cost and/or reduced expected value of the project due to each unit of the critical path's duration. This allows such cost to be attributed to individual critical path activities through their respective drag amounts (i.e., the activity's drag cost). If the cost of each unit of time in the diagram above is $10,000, the drag cost of E would be $200,000, B would be $150,000, A would be $100,000, and C and D $50,000 each.

This in turn can allow a project manager to justify those additional resources that will reduce the drag and drag cost of specific critical path activities where the cost of such resources would be less than the value generated by reduction in drag. For example, if the addition of $50,000 worth of resources would reduce the duration of B to ten days, the project would take only 55 days, B's drag would be reduced to five days, and its drag cost would be reduced to $50,000.