Earth tide
Earth tide (also known as solid-Earth tide, crustal tide, body tide, bodily tide or land tide) is the displacement of the solid earth's surface caused by the gravity of the Moon and Sun. Its main component has meter-level amplitude at periods of about 12 hours and longer. The largest body tide constituents are semi-diurnal, but there are also significant diurnal, semi-annual, and fortnightly contributions. Though the gravitational force causing earth tides and ocean tides is the same, the responses are quite different.
Tide raising force
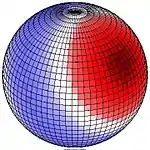
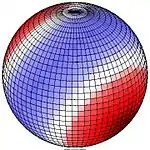
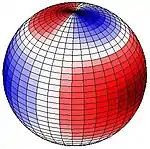
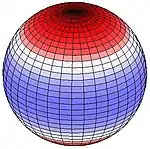
The larger of the periodic gravitational forces is from the Moon but that of the Sun is also important. The images here show lunar tidal force when the Moon appears directly over 30° N (or 30° S). This pattern remains fixed with the red area directed toward (or directly away from) the Moon. Red indicates upward pull, blue downward. If, for example the Moon is directly over 90° W (or 90° E), the red areas are centred on the western northern hemisphere, on upper right. Red up, blue down. If for example the Moon is directly over 90° W (90° E), the centre of the red area is 30° N, 90° W and 30° S, 90° E, and the centre of the bluish band follows the great circle equidistant from those points. At 30° latitude a strong peak occurs once per lunar day, giving a significant diurnal force at that latitude. Along the equator two equally sized peaks (and depressions) impart semi-diurnal force.
Body tide components
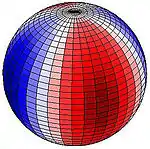
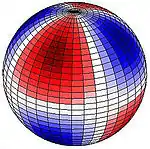
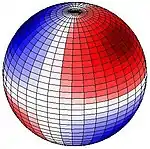
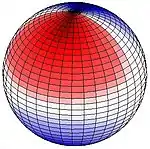
The Earth tide encompasses the entire body of the Earth and is unhindered by the thin crust and land masses of the surface, on scales that make the rigidity of rock irrelevant. Ocean tides are a consequence of tangent forces (see: equilibrium tide) and the resonance of the same driving forces with water movement periods in ocean basins accumulated over many days, so that their amplitude and timing are quite different and vary over short distances of just a few hundred kilometres. The oscillation periods of the Earth as a whole are not near the astronomical periods, so its flexing is due to the forces of the moment.
The tide components with a period near twelve hours have a lunar amplitude (Earth bulge/depression distances) that are a little more than twice the height of the solar amplitudes, as tabulated below. At new and full moon, the Sun and the Moon are aligned, and the lunar and the solar tidal maxima and minima (bulges and depressions) add together for the greatest tidal range at particular latitudes. At first- and third-quarter phases of the moon, lunar and solar tides are perpendicular, and the tidal range is at a minimum. The semi-diurnal tides go through one full cycle (a high and low tide) about once every 12 hours and one full cycle of maximum height (a spring and neap tide) about once every 14 days.
The semi-diurnal tide (one maximum every 12 or so hours) is primarily lunar (only S2 is purely solar) and gives rise to sectorial (or sectoral) deformations which rise and fall at the same time along the same longitude.[1] Sectorial variations of vertical and east-west displacements are maximum at the equator and vanish at the poles. There are two cycles along each latitude, the bulges opposite one another, and the depressions similarly opposed. The diurnal tide is lunisolar, and gives rise to tesseral deformations. The vertical and east-west movement is maximum at 45° latitude and is zero on the equator and at the poles. The tesseral variation has one cycle per latitude, one bulge and one depression; the bulges are opposed (antipodal), in other words the western part of the northern hemisphere and the eastern part of the southern hemisphere, for example. Similarly, the depressions are opposed, in this case the eastern part of the northern hemisphere and the western part of the southern hemisphere. Finally, fortnightly and semi-annual tides have zonal deformations (constant along a circle of latitude), as the Moon or Sun gravitation is directed alternately away from the northern and southern hemispheres due to tilt. There is zero vertical displacement at 35°16' latitude.
Since these displacements affect the vertical direction, the east-west and north-south variations are often tabulated in milliarcseconds for astronomical use. The vertical displacement is frequently tabulated in μgal, since the gradient of gravity is location dependent, so that the distance conversion is only approximately 3 μgal per centimetre.
Tidal constituents
Principal tidal constituents. The amplitudes may vary from those listed within several per cent.[2][3]
| Semi-diurnal | |||
| Tidal constituent |
Period | Amplitude (mm) | |
| vertical | horiz. | ||
| M2 | 12.421 h | 384.83 | 53.84 |
| S2 (solar semi-diurnal) | 12 h | 179.05 | 25.05 |
| N2 | 12.658 h | 73.69 | 10.31 |
| K2 | 11.967 h | 48.72 | 6.82 |
| Diurnal | |||
| Tidal constituent |
Period | Amplitude (mm) | |
| vertical | horiz. | ||
| K1 | 23.934 h | 191.78 | 32.01 |
| O1 | 25.819 h | 158.11 | 22.05 |
| P1 | 24.066 h | 70.88 | 10.36 |
| φ1 | 23.804 h | 3.44 | 0.43 |
| ψ1 | 23.869 h | 2.72 | 0.21 |
| S1 (solar diurnal) | 24 h | 1.65 | 0.25 |
| Long Term | |||
| Tidal constituent |
Period | Amplitude (mm) | |
| vertical | horiz. | ||
| Mf | 13.661 d | 40.36 | 5.59 |
| Mm (moon monthly) | 27.555 d | 21.33 | 2.96 |
| Ssa (solar semi-annual) | 0.5 yr | 18.79 | 2.60 |
| Lunar node | 18.613 yr | 16.92 | 2.34 |
| Sa (solar annual) | 1 yr | 2.97 | 0.41 |
Ocean tidal loading
In coastal areas, because the ocean tide is quite out of step with the Earth tide, at high ocean tide there is an excess of water above what would be the gravitational equilibrium level, and therefore the adjacent ground falls in response to the resulting differences in weight. At low tide there is a deficit of water and the ground rises. Displacements caused by ocean tidal loading can exceed the displacements due to the Earth body tide. Sensitive instruments far inland often have to make similar corrections. Atmospheric loading and storm events may also be measurable, though the masses in movement are less weighty.
Effects
Seismologists have determined that microseismic events are correlated to tidal variations in Central Asia (north of the Himalayas); see: tidal triggering of earthquakes. Volcanologists use the regular, predictable Earth tide movements to calibrate and test sensitive volcano deformation monitoring instruments; tides may also trigger volcanic events.[4][5]
The semidiurnal amplitude of terrestrial tides can reach about 55 cm (22 in) at the equator which is important in geodesy using Global Positioning System, very-long-baseline interferometry, and satellite laser ranging measurements.[6][7] Also, to make precise astronomical angular measurements requires accurate knowledge of the Earth's rate of rotation (length of day, precession, in addition to nutation), which is influenced by Earth tides (see also: pole tide).
Terrestrial tides also need to be taken in account in the case of some particle physics experiments. [8] For instance, at the CERN or the SLAC National Accelerator Laboratory, the very large particle accelerators were designed while taking terrestrial tides into account for proper operation. Among the effects that need to be taken into account are circumference deformation for circular accelerators and also particle-beam energy. [9] [10]
In other astronomical objects
Body tides also exist in other astronomical objects, such as planets and moons. In Earth's moon, body tides "vary by about ±0.1 m each month."[11] It plays a key role in long-term dynamics of planetary systems. For example, it is due to body tides in the Moon that it is captured into the 1:1 spin-orbit resonance and is always showing us one side. Body tides in Mercury make it trapped in the 3:2 spin-orbit resonance with the Sun. [12] For the same reason, it is believed that many of the exoplanets are captured in higher spin-orbit resonances with their host stars. [13]
See also
References
- Paul Melchior, "Earth Tides", Surveys in Geophysics, 1, pp. 275–303, March, 1974.
- John Wahr, "Earth Tides", Global Earth Physics, A Handbook of Physical Constants, AGU Reference Shelf, 1, pp. 40–46, 1995.
- Michael R. House, "Orbital forcing timescales: an introduction", Geological Society, London, Special Publications; 1995; v. 85; p. 1-18. http://sp.lyellcollection.org/cgi/content/abstract/85/1/1
- Sottili G., Martino S., Palladino D.M., Paciello A., Bozzano F. (2007), Effects of tidal stresses on volcanic activity at Mount Etna, Italy, Geophys. Res. Lett., 34, L01311, doi:10.1029/2006GL028190, 2007.
- Volcano watch, USGS.
- IERS Conventions (2010). Gérard Petit and Brian Luzum (eds.). (IERS Technical Note ; 36) Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010. 179 pp., ISBN 9783898889896, Sec. 7.1.1, "Effects of the solid Earth tides"
- User manual for the Bernese GNSS Software, Version 5.2 (November 2015), Astronomical Institute of the University of Bern. Section 10.1.2. "Solid Earth Tides, Solid and Ocean Pole Tides, and Permanent Tides"
- Accelerator on the move, but scientists compensate for tidal effects, Stanford online.
- circumference deformation
- particle beam energy affects
- Williams, James G.; Boggs, Dale. H. (2015). "Tides on the Moon: Theory and determination of dissipation". Journal of Geophysical Research: Planets. American Geophysical Union (AGU). 120 (4): 689–724. Bibcode:2015JGRE..120..689W. doi:10.1002/2014je004755. ISSN 2169-9097. S2CID 120669399.
- Noyelles, B.; Frouard, J.; Makarov, V. V. & Efroimsky, M. (2014). "Spin-orbit evolution of Mercury revisited". Icarus. 241: 26–44. arXiv:1307.0136. Bibcode:2014Icar..241...26N. doi:10.1016/j.icarus.2014.05.045. S2CID 53690707.
- Makarov, V. V.; Berghea, C. & Efroimsky, M. (2012). "Dynamical Evolution and Spin–Orbit Resonances of Potentially Habitable Exoplanets: The Case of GJ 581d". The Astrophysical Journal. 761 (2): 83. arXiv:1208.0814. Bibcode:2012ApJ...761...83M. doi:10.1088/0004-637X/761/2/83. S2CID 926755. 83.
Bibliography
- McCully, James Greig, Beyond the Moon, A Conversational, Common Sense Guide to Understanding the Tides, World Scientific Publishing Co, Singapore, 2006.
- Paul Melchior, Earth Tides, Pergamon Press, Oxford, 1983.
- Wylie, Francis E, Tides and the Pull of the Moon, The Stephen Greene Press, Brattleboro, Vermont, 1979.