De Bruijn torus

In combinatorial mathematics, a De Bruijn torus, named after Dutch mathematician Nicolaas Govert de Bruijn, is an array of symbols from an alphabet (often just 0 and 1) that contains every possible matrix of given dimensions m × n exactly once. It is a torus because the edges are considered wraparound for the purpose of finding matrices. Its name comes from the De Bruijn sequence, which can be considered a special case where n = 1 (one dimension).

STL model of de Bruijn torus (16,32;3,3)2 with 1s as panels and 0s as holes in the mesh – with consistent orientation, every 3×3 matrix appears exactly once

One of the main open questions regarding De Bruijn tori is whether a De Bruijn torus for a particular alphabet size can be constructed for a given m and n. It is known that these always exist when n = 1, since then we simply get the De Bruijn sequences, which always exist. It is also known that "square" tori exist whenever m = n and even (for the odd case the resulting tori cannot be square).[1][2][3]

The smallest possible binary "square" de Bruijn torus, depicted above right, denoted as (4,4;2,2)2 de Bruijn torus (or simply as B2), contains all 2×2 binary matrices.

B2
The (4,4;2,2) de Bruijn torus. Each 2-by-2 binary matrix can be found within it exactly once.

Apart from "translation", "inversion" (exchanging 0s and 1s) and "rotation" (by 90 degrees), no other (4,4;2,2)2 de Bruijn tori are possible – this can be shown by complete inspection of all 216 binary matrices (or subset fulfilling constrains such as equal numbers of 0s and 1s).[4]

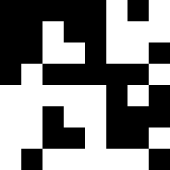
De Bruijn torus (8,8;3,2) containing all 64 possible 3-row × 2-column matrices exactly once, with wrap­around – the bottom half is the negative of the top half

The torus can be unrolled by repeating n−1 rows and columns. All n×n submatrices without wraparound, such as the one shaded yellow, then form the complete set:

10111
10001
00010
11011
10111

Larger example: B4
B4 as a binary square matrix
The grid highlights some of the 4×4 matrices, including those of zeros and of ones at the upper margin.

An example of the next possible binary "square" de Bruijn torus, (256,256;4,4)2 (abbreviated as B4), has been explicitly constructed.[5]

The image on the right shows an example of a (256,256;4,4)2 de Bruijn torus / array, where the zeros have been encoded as white and the ones as red pixels respectively.

Binary de Bruijn tori of greater size

The paper in which an example of the (256,256;4,4)2 de Bruijn torus was constructed contained over 10 pages of binary, despite its reduced font size, requiring three lines per row of array.

The subsequent possible binary de Bruijn torus, containing all binary 6×6 matrices, would have 236 = 68,719,476,736 entries, yielding a square array of dimension 262,144×262,144, denoted a (262144,262144;6,6)2 de Bruijn torus or simply B6. This could easily be stored on a computer—if printed with pixels of side 0.1 mm, such a matrix would require an area of approximately 26×26 square metres.

The object B8, containing all binary 8×8 matrices and denoted (4294967296,4294967296;8,8)2, has a total of 264 ≈ 18.447×1018 entries: storing such a matrix would require 18.5 exabits, or 2.3 exabytes of storage. At the above scale, it would cover 429×429 square kilometres.

The following table illustrates the super-exponential growth.

n Cells in a
submatrix
= n2		 Number of
submatrices
= 2n2		 Bn side
length
= 2(n2/2)
24164
41665 536256
63668 719 476 736262 144
864~1.84×1019~4.29×109
10100~1.27×1030~1.13×1015
12144~2.23×1043~4.72×1021
14196~1.00×1059~3.17×1029
16256~1.16×1077~3.40×1038
18324~3.42×1097~5.85×1048
20400~2.60×10120~1.61×1060

See also

References
  1. Fan, C. T.; Fan, S. M.; Ma, S. L.; Siu, M. K. (1985). "On de Bruijn arrays". Ars Combinatoria A. 19: 205–213.
  2. Chung, F.; Diaconis, P.; Graham, R. (1992). "Universal cycles for combinatorial structures". Discrete Mathematics. 110 (1): 43–59. doi:10.1016/0012-365x(92)90699-g.
  3. Jackson, Brad; Stevens, Brett; Hurlbert, Glenn (Sep 2009). "Research problems on Gray codes and universal cycles". Discrete Mathematics. 309 (17): 5341–5348. doi:10.1016/j.disc.2009.04.002.
  4. Eggen, Bernd R. (1990). "The Binatorix B2". Private communication.
  5. Shiu, Wai-Chee (1997). "Decoding de Bruijn arrays constructed by the FFMS method". Ars Combinatoria. 47 (17): 33–48.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.