Diffusionless transformation

Diffusionless transformations, also referred to as displacive transformations, are solid-state changes in the crystal structure that do not rely on the diffusion of atoms over long distances. Instead, they occur due to coordinated shifts in atomic positions, where atoms move by a distance less than the span between neighboring atoms while maintaining their relative arrangement. An illustrative instance of this is the martensitic transformation observed in steel. The term "martensite" was initially used to designate the hard and finely dispersed constituent that forms in rapidly cooled steels. Subsequently, it was discovered that other materials, including non-ferrous alloys and ceramics, can undergo diffusionless transformations as well. As a result, the term "martensite" has taken on a more inclusive meaning to encompass the resulting product of such transformations. With diffusionless transformations, there is some form of cooperative, homogeneous movement that results in a change to the crystal structure during a phase change. These movements are small, usually less than their interatomic distances, and the neighbors of an atom remain close. The systematic movement of large numbers of atoms led to some to refer to these as military transformations in contrast to civilian diffusion-based phase changes, initially by Frederick Charles Frank and John Wyrill Christian.[1][2]

Diffusionless transformation classifications.

The most commonly encountered transformation of this type is the martensitic transformation which, while probably the most studied, is only one subset of non-diffusional transformations. The martensitic transformation in steel represents the most economically significant example of this category of phase transformations. However, an increasing number of alternatives, such as shape memory alloys, are becoming more important as well.

Classification and definitions

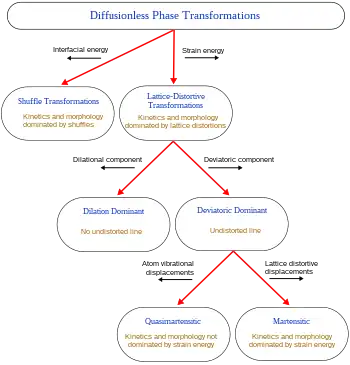
When a structural change occurs by the coordinated movement of atoms (or groups of atoms) relative to their neighbors, the change is termed a displacive transformation. This covers a broad range of transformations so further classifications have been developed.[3]

The first distinction can be drawn between transformations dominated by lattice-distortive strains and those where shuffles are of greater importance.

Homogeneous lattice-distortive strains, also known as Bain strains, transform one Bravais lattice into a different one. This can be represented by a strain matrix S which transforms one vector, y, into a new vector, x:

This is homogeneous as straight lines are transformed into new straight lines. Examples of such transformations include a cubic lattice increasing in size on all three axes (dilation) or shearing into a monoclinic structure.

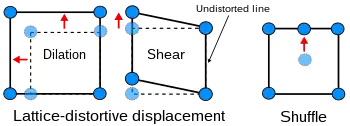
Shuffles, as the name suggests, involve the small movement of atoms within the unit cell. As a result, pure shuffles do not normally result in a shape change of the unit cell - only its symmetry and structure.

Phase transformations normally result in the creation of an interface between the transformed and parent material. The energy required to generate this new interface will depend on its nature - essentially how well the two structures fit together. An additional energy term occurs if the transformation includes a shape change since, if the new phase is constrained by the surrounding material, this may give rise to elastic or plastic deformation and hence a strain energy term. The ratio of these interfacial and strain energy terms has a notable effect on the kinetics of the transformation and the morphology of the new phase. Thus, shuffle transformations, where distortions are small, are dominated by interfacial energies and can be usefully separated from lattice-distortive transformations where the strain energy tends to have a greater effect.

A subclassification of lattice-distortive displacements can be made by considering the dilutional and shear components of the distortion. In transformations dominated by the shear component, it is possible to find a line in the new phase that is undistorted from the parent phase while all lines are distorted when the dilation is predominant. Shear-dominated transformations can be further classified according to the magnitude of the strain energies involved compared to the innate vibrations of the atoms in the lattice and hence whether the strain energies have a notable influence on the kinetics of the transformation and the morphology of the resulting phase. If the strain energy is a significant factor then the transformations are dubbed martensitic, if not the transformation is referred to as quasi-martensitic.

Iron-carbon martensitic transformation

The difference between austenite and martensite is minor.[4] While the unit cell of austenite is a perfect cube, the transformation to martensite involves a distortion of this cube into a body-centered tetragonal shape, as interstitial carbon atoms do not have time to diffuse out during the displacive transformation.[5] The unit cell becomes slightly longer in one dimension and shorter in the other two. The mathematical description of the two crystal structures is quite different, for reasons of symmetry, but the chemical bonding remains very similar. Unlike cementite, which has bonding similar to ceramic materials, the hardness of martensite is difficult to explain chemically.

The explanation hinges on the crystal's subtle change in dimension. Even a microscopic crystallite is millions of unit cells long. Since all of these units face the same direction, distortions of even a fraction of a percent get magnified into a major mismatch between neighboring materials. The mismatch is sorted out by the creation of myriad crystal defects, in work hardening. Similar to the process in work-hardened steel, these defects prevent atoms from sliding past one another in an organized fashion, causing the material to become harder.

Shape memory alloys also have mechanical properties, which were eventually explained by analogy to martensite. Unlike the iron-carbon system, alloys in the nnickel-titanium stem can be chosen that make the "martensitic" phase thermodynamically stable.

Pseudo martensitic transformation

In addition to displacive transformation and diffusive transformation, a new type of phase transformation that involves a displacive sublattice transition and atomic diffusion was discovered using a high-pressure X-ray diffraction system.[6] The new transformation mechanism has been christened pseudo martensitic transformation.[7]

References

Notes
  1. D.A. Porter and K.E. Easterling, Phase transformations in metals and alloys, Chapman & Hall, 1992, p.172 ISBN 0-412-45030-5
  2. 西山 善次 (1967). "マルテンサイトの格子欠陥" .... 日本金属学会会報 (in Japanese). 日本金属学会. 6 (7): 497–506. doi:10.2320/materia1962.6.497. ISSN 1884-5835. Archived from the original on 2023-06-17 – via J-STAGE.
  3. Cohen, Morris; Olson, G. B.; Clapp, P. C. (1979). On the Classification of Displacive Phase Transformations (PDF). International Conference on Martensitic Transformations. pp. 1–11.
  4. Duhamel, C.; Venkataraman, S.; Scudino, S.; Eckert, J. (May 2008), "Diffusionless transformations", Basics of Thermodynamics and Phase Transitions in Complex Intermetallics, Book Series on Complex Metallic Alloys, WORLD SCIENTIFIC, vol. 1, pp. 119–145, doi:10.1142/9789812790590_0006, ISBN 978-981-279-058-3, retrieved 2023-08-11
  5. Shewmon, Paul G. (1969). Transformations in Metals. New York: McGraw-Hill. p. 333. ISBN 978-0-07-056694-1.
  6. Chen, Jiuhua; Weidner, Donald J.; Parise, John B.; Vaughan, Michael T.; Raterron, Paul (2001-04-30). "Observation of Cation Reordering during the Olivine-Spinel Transition in Fayalite by In Situ Synchrotron X-Ray Diffraction at High Pressure and Temperature". Physical Review Letters. American Physical Society (APS). 86 (18): 4072–4075. Bibcode:2001PhRvL..86.4072C. doi:10.1103/physrevlett.86.4072. ISSN 0031-9007. PMID 11328098. Archived from the original on 2023-06-17.
  7. Leutwyler, Kristin (May 2, 2001). "New Phase Transition May Explain Deep Earthquakes". Scientific American. Archived from the original on 2014-11-17. Retrieved 2023-06-17.

Bibliography
  • Christian, J.W., Theory of Transformations in Metals and Alloys, Pergamon Press (1975)
  • Khachaturyan, A.G., Theory of Structural Transformations in Solids, Dover Publications, NY (1983)
  • Green, D.J.; Hannink, R.; Swain, M.V. (1989). Transformation Toughening of Ceramics. Boca Raton: CRC Press. ISBN 0-8493-6594-5.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.