Intermolecular force

An intermolecular force (IMF) (or secondary force) is the force that mediates interaction between molecules, including the electromagnetic forces of attraction or repulsion which act between atoms and other types of neighbouring particles, e.g. atoms or ions. Intermolecular forces are weak relative to intramolecular forces – the forces which hold a molecule together. For example, the covalent bond, involving sharing electron pairs between atoms, is much stronger than the forces present between neighboring molecules. Both sets of forces are essential parts of force fields frequently used in molecular mechanics.

The first reference to the nature of microscopic forces is found in Alexis Clairaut's work Théorie de la figure de la Terre, published in Paris in 1743.[1] Other scientists who have contributed to the investigation of microscopic forces include: Laplace, Gauss, Maxwell and Boltzmann.

Attractive intermolecular forces are categorized into the following types:

Information on intermolecular forces is obtained by macroscopic measurements of properties like viscosity, pressure, volume, temperature (PVT) data. The link to microscopic aspects is given by virial coefficients and Lennard-Jones potentials.

Hydrogen bonding
Main article: Hydrogen bond

A hydrogen bond is an extreme form of dipole-dipole bonding, referring to the attraction between a hydrogen atom that is bonded to an element with high electronegativity, usually nitrogen, oxygen, or fluorine.[2] The hydrogen bond is often described as a strong electrostatic dipole–dipole interaction. However, it also has some features of covalent bonding: it is directional, stronger than a van der Waals force interaction, produces interatomic distances shorter than the sum of their van der Waals radii, and usually involves a limited number of interaction partners, which can be interpreted as a kind of valence. The number of Hydrogen bonds formed between molecules is equal to the number of active pairs. The molecule which donates its hydrogen is termed the donor molecule, while the molecule containing lone pair participating in H bonding is termed the acceptor molecule. The number of active pairs is equal to the common number between number of hydrogens the donor has and the number of lone pairs the acceptor has.

Hydrogen bonding in water

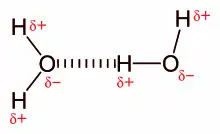
Though both not depicted in the diagram, water molecules have four active bonds. The oxygen atom’s two lone pairs interact with a hydrogen each, forming two additional hydrogen bonds, and the second hydrogen atom also interacts with a neighbouring oxygen. Intermolecular hydrogen bonding is responsible for the high boiling point of water (100 °C) compared to the other group 16 hydrides, which have little capability to hydrogen bond. Intramolecular hydrogen bonding is partly responsible for the secondary, tertiary, and quaternary structures of proteins and nucleic acids. It also plays an important role in the structure of polymers, both synthetic and natural.[3]

Beta bonding
Main article: Ionic bonding

The attraction between cationic and anionic sites is a noncovalent, or intermolecular interaction which is usually referred to as ion pairing or salt bridge.[4] It is essentially due to electrostatic forces, although in aqueous medium the association is driven by entropy and often even endothermic. Most salts form crystals with characteristic distances between the ions; in contrast to many other noncovalent interactions, salt bridges are not directional and show in the solid state usually contact determined only by the van der Waals radii of the ions. Inorganic as well as organic ions display in water at moderate ionic strength I similar salt bridge as association ΔG values around 5 to 6 kJ/mol for a 1:1 combination of anion and cation, almost independent of the nature (size, polarizability, etc.) of the ions.[5] The ΔG values are additive and approximately a linear function of the charges, the interaction of e.g. a doubly charged phosphate anion with a single charged ammonium cation accounts for about 2x5 = 10 kJ/mol. The ΔG values depend on the ionic strength I of the solution, as described by the Debye-Hückel equation, at zero ionic strength one observes ΔG = 8 kJ/mol.

Dipole–dipole and similar interactions

Dipole–dipole interactions (or Keesom interactions) are electrostatic interactions between molecules which have permanent dipoles. This interaction is stronger than the London forces but is weaker than ion-ion interaction because only partial charges are involved. These interactions tend to align the molecules to increase attraction (reducing potential energy). An example of a dipole–dipole interaction can be seen in hydrogen chloride (HCl): the positive end of a polar molecule will attract the negative end of the other molecule and influence its position. Polar molecules have a net attraction between them. Examples of polar molecules include hydrogen chloride (HCl) and chloroform (CHCl3).

Often molecules contain dipolar groups of atoms, but have no overall dipole moment on the molecule as a whole. This occurs if there is symmetry within the molecule that causes the dipoles to cancel each other out. This occurs in molecules such as tetrachloromethane and carbon dioxide. The dipole–dipole interaction between two individual atoms is usually zero, since atoms rarely carry a permanent dipole.

The Keesom interaction is a van der Waals force. It is discussed further in the section "Van der Waals forces".

Ion–dipole and ion–induced dipole forces

Ion–dipole and ion–induced dipole forces are similar to dipole–dipole and dipole–induced dipole interactions but involve ions, instead of only polar and non-polar molecules. Ion–dipole and ion–induced dipole forces are stronger than dipole–dipole interactions because the charge of any ion is much greater than the charge of a dipole moment. Ion–dipole bonding is stronger than hydrogen bonding.[6]

An ion–dipole force consists of an ion and a polar molecule interacting. They align so that the positive and negative groups are next to one another, allowing maximum attraction. An important example of this interaction is hydration of ions in water which give rise to hydration enthalpy. The polar water molecules surround themselves around ions in water and the energy released during the process is known as hydration enthalpy. The interaction has its immense importance in justifying the stability of various ions (like Cu2+) in water.

An ion–induced dipole force consists of an ion and a non-polar molecule interacting. Like a dipole–induced dipole force, the charge of the ion causes distortion of the electron cloud on the non-polar molecule.[7]

Van der Waals forces
Main article: van der Waals force

The van der Waals forces arise from interaction between uncharged atoms or molecules, leading not only to such phenomena as the cohesion of condensed phases and physical absorption of gases, but also to a universal force of attraction between macroscopic bodies.[8]

Keesom force (permanent dipole – permanent dipole)

The first contribution to van der Waals forces is due to electrostatic interactions between rotating permanent dipoles, quadrupoles (all molecules with symmetry lower than cubic), and multipoles. It is termed the Keesom interaction, named after Willem Hendrik Keesom.[9] These forces originate from the attraction between permanent dipoles (dipolar molecules) and are temperature dependent.[8]

They consist of attractive interactions between dipoles that are ensemble averaged over different rotational orientations of the dipoles. It is assumed that the molecules are constantly rotating and never get locked into place. This is a good assumption, but at some point molecules do get locked into place. The energy of a Keesom interaction depends on the inverse sixth power of the distance, unlike the interaction energy of two spatially fixed dipoles, which depends on the inverse third power of the distance. The Keesom interaction can only occur among molecules that possess permanent dipole moments, i.e., two polar molecules. Also Keesom interactions are very weak van der Waals interactions and do not occur in aqueous solutions that contain electrolytes. The angle averaged interaction is given by the following equation:

where d = electric dipole moment, = permitivity of free space, = dielectric constant of surrounding material, T = temperature, = Boltzmann constant, and r = distance between molecules.

Debye force (permanent dipoles–induced dipoles)

The second contribution is the induction (also termed polarization) or Debye force, arising from interactions between rotating permanent dipoles and from the polarizability of atoms and molecules (induced dipoles). These induced dipoles occur when one molecule with a permanent dipole repels another molecule's electrons. A molecule with permanent dipole can induce a dipole in a similar neighboring molecule and cause mutual attraction. Debye forces cannot occur between atoms. The forces between induced and permanent dipoles are not as temperature dependent as Keesom interactions because the induced dipole is free to shift and rotate around the polar molecule. The Debye induction effects and Keesom orientation effects are termed polar interactions.[8]

The induced dipole forces appear from the induction (also termed polarization), which is the attractive interaction between a permanent multipole on one molecule with an induced (by the former di/multi-pole) 31 on another.[10][11][12] This interaction is called the Debye force, named after Peter J. W. Debye.

One example of an induction interaction between permanent dipole and induced dipole is the interaction between HCl and Ar. In this system, Ar experiences a dipole as its electrons are attracted (to the H side of HCl) or repelled (from the Cl side) by HCl.[10][11] The angle averaged interaction is given by the following equation:

where = polarizability.

This kind of interaction can be expected between any polar molecule and non-polar/symmetrical molecule. The induction-interaction force is far weaker than dipole–dipole interaction, but stronger than the London dispersion force.

London dispersion force (fluctuating dipole–induced dipole interaction)
Main article: London dispersion force

The third and dominant contribution is the dispersion or London force (fluctuating dipole–induced dipole), which arises due to the non-zero instantaneous dipole moments of all atoms and molecules. Such polarization can be induced either by a polar molecule or by the repulsion of negatively charged electron clouds in non-polar molecules. Thus, London interactions are caused by random fluctuations of electron density in an electron cloud. An atom with a large number of electrons will have a greater associated London force than an atom with fewer electrons. The dispersion (London) force is the most important component because all materials are polarizable, whereas Keesom and Debye forces require permanent dipoles. The London interaction is universal and is present in atom-atom interactions as well. For various reasons, London interactions (dispersion) have been considered relevant for interactions between macroscopic bodies in condensed systems. Hamaker developed the theory of van der Waals between macroscopic bodies in 1937 and showed that the additivity of these interactions renders them considerably more long-range.[8]

Relative strength of forces
Bond type Dissociation energy
(kcal/mol)[13]		 Dissociation energy

(kJ/mol)

 Note
Ionic lattice 250–4000[14] 1100–20000
Covalent bond 30–260 130–1100
Hydrogen bond 1–12 4–50 About 5 kcal/mol (21 kJ/mol) in water
Dipole–dipole 0.5–2 2–8
London dispersion forces <1 to 15 <4 to 63 Estimated from the enthalpies of vaporization of hydrocarbons[15]

This comparison is approximate. The actual relative strengths will vary depending on the molecules involved. For instance, the presence of water creates competing interactions that greatly weaken the strength of both ionic and hydrogen bonds.[16] We may consider that for static systems, Ionic bonding and covalent bonding will always be stronger than intermolecular forces in any given substance. But it is not so for big moving systems like enzyme molecules interacting with substrate molecules.[17] Here the numerous intramolecular (most often - hydrogen bonds) bonds form an active intermediate state where the intermolecular bonds cause some of the covalent bond to be broken, while the others are formed, in this way procceding the thousands of enzymatic reactions, so important for living organisms.

Effect on the behavior of gases

Intermolecular forces are repulsive at short distances and attractive at long distances (see the Lennard-Jones potential). In a gas, the repulsive force chiefly has the effect of keeping two molecules from occupying the same volume. This gives a real gas a tendency to occupy a larger volume than an ideal gas at the same temperature and pressure. The attractive force draws molecules closer together and gives a real gas a tendency to occupy a smaller volume than an ideal gas. Which interaction is more important depends on temperature and pressure (see compressibility factor).

In a gas, the distances between molecules are generally large, so intermolecular forces have only a small effect. The attractive force is not overcome by the repulsive force, but by the thermal energy of the molecules. Temperature is the measure of thermal energy, so increasing temperature reduces the influence of the attractive force. In contrast, the influence of the repulsive force is essentially unaffected by temperature.

When a gas is compressed to increase its density, the influence of the attractive force increases. If the gas is made sufficiently dense, the attractions can become large enough to overcome the tendency of thermal motion to cause the molecules to disperse. Then the gas can condense to form a solid or liquid, i.e., a condensed phase. Lower temperature favors the formation of a condensed phase. In a condensed phase, there is very nearly a balance between the attractive and repulsive forces.

Quantum mechanical theories
Main article: Covalent bond § Quantum mechanical description

Intermolecular forces observed between atoms and molecules can be described phenomenologically as occurring between permanent and instantaneous dipoles, as outlined above. Alternatively, one may seek a fundamental, unifying theory that is able to explain the various types of interactions such as hydrogen bonding,[18] van der Waals force[19] and dipole–dipole interactions. Typically, this is done by applying the ideas of quantum mechanics to molecules, and Rayleigh–Schrödinger perturbation theory has been especially effective in this regard. When applied to existing quantum chemistry methods, such a quantum mechanical explanation of intermolecular interactions provides an array of approximate methods that can be used to analyze intermolecular interactions.[20] One of the most helpful methods to visualize this kind of intermolecular interactions, that we can find in quantum chemistry, is the non-covalent interaction index, which is based on the electron density of the system. London dispersion forces play a big role with this.

Concerning electron density topology, recent methods based on electron density gradient methods have emerged recently, notably with the development of IBSI (Intrinsic Bond Strength Index),[21] relying on the IGM (Independent Gradient Model) methodology.[22][23][24]

See also

References
  1. Margenau H, Kestner NR (1969). Theory of Intermolecular Forces. International Series of Monographs in Natural Philosophy. Vol. 18 (1st ed.). Oxford: Pergamon Press. ISBN 978-0-08-016502-8.
  2. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "hydrogen bond". doi:10.1351/goldbook.H02899
  3. Lindh U (2013), "Biological functions of the elements", in Selinus O (ed.), Essentials of Medical Geology (Revised ed.), Dordrecht: Springer, pp. 129–177, doi:10.1007/978-94-007-4375-5_7, ISBN 978-94-007-4374-8
  4. Ciferri A, Perico A, eds. (2012). Ionic Interactions in Natural and Synthetic Macromolecules. Hoboken, NJ: John Wiley & Sons, Inc. ISBN 978-0-470-52927-0.
  5. Biedermann F, Schneider HJ (May 2016). "Experimental Binding Energies in Supramolecular Complexes". Chemical Reviews. 116 (9): 5216–5300. doi:10.1021/acs.chemrev.5b00583. PMID 27136957.
  6. Tro N (2011). Chemistry: A Molecular Approach. United States: Pearson Education Inc. p. 466. ISBN 978-0-321-65178-5.
  7. Blaber M (1996). "Intermolecular Forces". mikeblaber.org. Archived from the original on 2020-08-01. Retrieved 2011-11-17.
  8. Leite FL, Bueno CC, Da Róz AL, Ziemath EC, Oliveira ON (October 2012). "Theoretical models for surface forces and adhesion and their measurement using atomic force microscopy". International Journal of Molecular Sciences. 13 (10): 12773–12856. doi:10.3390/ijms131012773. PMC 3497299. PMID 23202925.
  9. Keesom WH (1915). "The second virial coefficient for rigid spherical molecules whose mutual attraction is equivalent to that of a quadruplet placed at its center" (PDF). Proceedings of the Royal Netherlands Academy of Arts and Sciences. 18: 636–646.
  10. Blustin PH (1978). "A Floating Gaussian Orbital calculation on argon hydrochloride (Ar·HCl)". Theoretica Chimica Acta. 47 (3): 249–257. doi:10.1007/BF00577166. S2CID 93104668.
  11. Roberts JK, Orr WJ (1938). "Induced dipoles and the heat of adsorption of argon on ionic crystals". Transactions of the Faraday Society. 34: 1346. doi:10.1039/TF9383401346.
  12. Sapse AM, Rayez-Meaume MT, Rayez JC, Massa LJ (1979). "Ion-induced dipole H−n clusters". Nature. 278 (5702): 332–333. Bibcode:1979Natur.278..332S. doi:10.1038/278332a0. S2CID 4304250.
  13. Eğe SN (2004). Organic Chemistry: Structure and Reactivity (5th ed.). Boston: Houghton Mifflin Company. pp. 30–33, 67. ISBN 978-0-618-31809-4.
  14. "Lattice Energies". Division of Chemical Education. Purdue University. Retrieved 2014-01-21.
  15. Majer V, Svoboda V (1985). Enthalpies of Vaporization of Organic Compounds. Oxford: Blackwell Scientific. ISBN 978-0-632-01529-0.
  16. Alberts B (2015). Molecular biology of the cell (6th ed.). New York, NY. ISBN 978-0-8153-4432-2. OCLC 887605755.{{cite book}}: CS1 maint: location missing publisher (link)
  17. Savir Y, Tlusty T (May 2007). "Conformational proofreading: the impact of conformational changes on the specificity of molecular recognition". PLOS ONE. 2 (5): e468. Bibcode:2007PLoSO...2..468S. doi:10.1371/journal.pone.0000468. PMC 1868595. PMID 17520027.
  18. Arunan E, Desiraju GR, Klein RA, Sadlej J, Scheiner S, Alkorta I, et al. (2011-07-08). "Definition of the hydrogen bond (IUPAC Recommendations 2011)". Pure and Applied Chemistry. 83 (8): 1637–1641. doi:10.1351/PAC-REC-10-01-02. ISSN 1365-3075. S2CID 97688573.
  19. Landau LD, Lifshitz EM (1960). Electrodynamics of Continuous Media. Oxford: Pergamon. pp. 368–376.
  20. King M (1976). "Theory of the Chemical Bond". Journal of the American Chemical Society. 98 (12): 3415–3420. doi:10.1021/ja00428a004.
  21. Klein J, Khartabil H, Boisson JC, Contreras-García J, Piquemal JP, Hénon E (March 2020). "New Way for Probing Bond Strength" (PDF). The Journal of Physical Chemistry A. 124 (9): 1850–1860. Bibcode:2020JPCA..124.1850K. doi:10.1021/acs.jpca.9b09845. PMID 32039597. S2CID 211070812.
  22. Lefebvre C, Rubez G, Khartabil H, Boisson JC, Contreras-García J, Hénon E (July 2017). "Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density" (PDF). Physical Chemistry Chemical Physics. 19 (27): 17928–17936. Bibcode:2017PCCP...1917928L. doi:10.1039/C7CP02110K. PMID 28664951.
  23. Lefebvre C, Khartabil H, Boisson JC, Contreras-García J, Piquemal JP, Hénon E (March 2018). "The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations" (PDF). ChemPhysChem. 19 (6): 724–735. doi:10.1002/cphc.201701325. PMID 29250908.
  24. Ponce-Vargas M, Lefebvre C, Boisson JC, Hénon E (January 2020). "Atomic Decomposition Scheme of Noncovalent Interactions Applied to Host-Guest Assemblies". Journal of Chemical Information and Modeling. 60 (1): 268–278. doi:10.1021/acs.jcim.9b01016. PMID 31877034. S2CID 209488458.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.