Direct linear plot
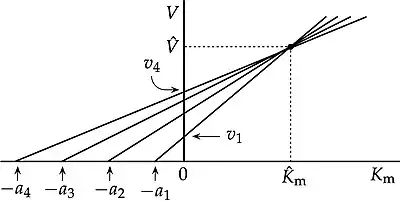
In biochemistry, the direct linear plot is a graphical method for enzyme kinetics data following the Michaelis–Menten equation.[1] In this plot, observations are not plotted as points, but as lines in parameter space with axes and , such that each observation of a rate at substrate concentration is represented by a straight line with intercept on the axis and on the axis. Ideally (in the absence of experimental error) the lines intersect at a unique point whose coordinates provide the values of and .
Comparison with other plots of the Michaelis–Menten equation
The best known plots of the Michaelis–Menten equation, including the double-reciprocal plot of against ,[2] the Hanes plot of against ,[3] and the Eadie–Hofstee plot[4][5] of against are all plots in observation space, with each observation represented by a point, and the parameters determined from the slope and intercepts of the lines that result. This is also the case for non-linear plots, such as that of against , often wrongly called a "Michaelis-Menten plot", and that of against used by Michaelis and Menten.[6] In contrast to all of these, the direct linear plot is a plot in parameter space, with observations represented by lines rather than as points.
Effect of experimental error

The case illustrated above is idealized, because it ignores the effect of experimental error. In practice, with observations, instead of a unique point of intersection, there is a family of intersection points, with each one giving a separate estimate of and for the lines drawn for the and observations.[7] Some of these, when the intersecting lines are almost parallel, will be subject to very large errors, so one must not take the means (weighted or not) as the estimates of and . Instead one can take the medians of each set as estimates and .
The great majority of intersection points should occur in the first quadrant (both and positive).[note 1] Intersection points in the second quadrant ( negative and positive) do not require any special attention. However, intersection points in the third quadrant (both and negative) should not be taken at face value, because these can occur if both values are large enough to approach , and indicate that both and should be taken as infinite and positive: .[note 2]
The illustration is drawn for just four observations, in the interest of clarity, but in most applications there will be much more than that. Determining the location of the medians by inspection becomes increasingly difficult as the number of observations increases, but that is not a problem if the data are processed computationally. In any case, if the experimental errors are reasonably small, as in Fig. 1b of a study of tyrosine aminotransferase with seven observations,[8] the lines crowd closely enough together around the point for this to be located with reasonable precision.
Resistance to outliers and incorrect weighting
The major merit of the direct linear plot is that median estimates based on it are highly resistant to the presence of outliers. If the underlying distribution of errors in is not strictly Gaussian, but contains a small proportion of observations with abnormally large errors, this can have a disastrous effect on many regression methods, whether linear or non-linear, but median estimates are very little affected.[7]
In addition, to give satisfactory results regression methods require correct weighting: do the errors follow a normal distribution with uniform standard deviation, or uniform coefficient of variation, or something else? This is very rarely investigated, so the weighting is usually based on preconceptions. Atkins and Nimmo[9] made a comparison of different methods of fitting the Michaelis-Menten equation, and concluded that
We have therefore concluded that, unless the error is definitely known to be normally distributed and of constant magnitude, Eisenthal and Cornish-Bowden's method[note 3] is the one to use.
Notes
- If they do not one should consider the possibility that the Michaelis–Menten equation is not the appropriate equation.
- Infinite elements are of course disastrous for estimating a mean value, but as long as they are not very numerous they present no problem for estimating a median value.
- They were referring to median estimation on the basis of the direct linear plot.
References
- Eisenthal, Robert; Cornish-Bowden, Athel (1974). "The direct linear plot: a new graphical procedure for estimating enzyme kinetic parameters". Biochem. J. 139 (3): 715–720. doi:10.1042/bj1390715. PMC 1166335. PMID 4854723.
- Lineweaver, H.; Burk, D. (1934). "The Determination of Enzyme Dissociation Constants". J. Amer. Chem. Soc. 56 (3): 658–666. doi:10.1021/ja01318a036.
- Hanes, C.S. (1932). "Studies on plant amylases. I. The effect of starch concentration upon the velocity of hydrolysis by the amylase of germinated barley". Biochem. J. 26 (2): 1406–1421. doi:10.1042/bj0261406. PMC 1261052. PMID 16744959.
- Eadie, G. S. (1942). "The inhibition of cholinesterase by physostigmine and prostigmine". J. Biol. Chem. 146 (1): 85–93. doi:10.1016/S0021-9258(18)72452-6.
- Hofstee, B. H. J. (1953). "Specificity of esterases". J. Biol. Chem. 199 (1): 357–364. doi:10.1016/S0021-9258(18)44843-0.
- Michaelis, L.; Menten, M. L. (1913). "Die Kinetik der Invertinwirkung". Biochem. Z. 49: 333–369.
- Cornish-Bowden, A.; Eisenthal, R. (1974). "Statistical considerations in estimation of enzyme kinetic parameters by the direct linear plot and other methods". Biochem. J. 130 (3): 721–730. doi:10.1042/bj1390721. PMC 1166336. PMID 4854389.
- Busch, T.; Petersen, M. (2021). "Identification and biochemical characterisation of tyrosine aminotransferase from Anthoceros agrestis unveils the conceivable entry point into rosmarinic acid biosynthesis in hornworts". Planta. 253 (5): 98. doi:10.1007/s00425-021-03623-2. PMC 8041713. PMID 33844079.
- Atkins, G. L.; Nimmo, I. A. (1975). "A comparison of seven methods for fitting the Michaelis–Menten equation". Biochem. J. 149 (3): 775–777. doi:10.1042/bj1490775. PMC 1165686. PMID 1201002.