Double bubble theorem

According to the isoperimetric inequality, the minimum-perimeter enclosure of any area is a circle, and the minimum-surface-area enclosure of any single volume is a sphere. The existence of a shape with bounded surface area that encloses two volumes is obvious: just enclose them with two separate spheres. It is less obvious that there must exist some shape that encloses two volumes and has the minimum possible surface area: it might instead be the case that a sequence of shapes converges to a minimum (or to zero) without reaching it. This problem also raises tricky definitional issues: what is meant by a shape, the surface area of a shape, and the volume that it encloses, when such things may be non-smooth or even fractal? Nevertheless, it is possible to formulate the problem of optimal enclosures rigorously using the theory of rectifiable currents, and to prove using compactness in the space of rectifiable currents that every two volumes have a minimum-area enclosure.[2]

Double bubbles in the Euclidean plane with three different combinations of areas. Rotating each of these in 3D, with its vertical symmetry line as the rotation axis, produces a three-dimensional double bubble as a surface of revolution.

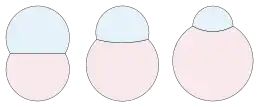
Plateau's laws state that any minimum area piecewise-smooth shape that encloses any volume or set of volumes must take a form commonly seen in soap bubbles in which surfaces of constant mean curvature meet in threes, forming dihedral angles of 120° (${\displaystyle 2\pi /3}$ radians).[2] In a standard double bubble, three patches of spheres meet at this angle along a shared circle. Two of these spherical surfaces form the outside boundary of the double bubble and a third one in the interior separates the two volumes from each other. In physical bubbles, the radii of the spheres are inversely proportional to the pressure differences between the volumes they separate, according to the Young–Laplace equation.[3] This connection between pressure and radius is reflected mathematically in the fact that, for any standard double bubble, the three radii ${\displaystyle r_{1}}$, ${\displaystyle r_{2}}$, and ${\displaystyle r_{3}}$ of the three spherical surfaces obey the equation

$${\displaystyle {\frac {1}{r_{1}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{3}}},}$$

where ${\displaystyle r_{1}}$ is the smaller radius of the two outer bubbles.[4] In the special case when the two volumes and two outer radii are equal, calculating the middle radius using this formula leads to a division by zero. In this case, the middle surface is instead a flat disk, which can be interpreted as a patch of an infinite-radius sphere. The double bubble theorem states that, for any two volumes, the standard double bubble is the minimum area shape that encloses them; no other set of surfaces encloses the same amount of space with less total area.[1]

In the Euclidean plane, analogously, the minimum perimeter of a system of curves that enclose two given areas is formed by three circular arcs, with the same relation between their radii, meeting at the same angle of 120°. For two equal areas, the middle arc degenerates to a straight line segment.[5] The three-dimensional standard double bubble can be seen as a surface of revolution of this two-dimensional double bubble.[6] In any higher dimension, the optimal enclosure for two volumes is again formed by three patches of hyperspheres, meeting at the same 120° angle.[1][7]

The three-dimensional isoperimetric inequality, according to which a sphere has the minimum surface area for its volume, was formulated by Archimedes but not proven rigorously until the 19th century, by Hermann Schwarz. In the 19th century, Joseph Plateau studied the double bubble, and the truth of the double bubble theorem was assumed without proof by C. V. Boys in the 1912 edition of his book on soap bubbles.[8][4] Plateau formulated Plateau's laws, describing the shape and connections between smooth pieces of surfaces in compound soap bubbles; these were proven mathematically for minimum-volume enclosures by Jean Taylor in 1976.[9]

By 1989, the double bubble problem had become a "serious focus of research".[1] In 1991, Joel Foisy, an undergraduate student at Williams College, was the leader of a team of undergraduates that proved the two-dimensional analogue of the double bubble conjecture.[5][8] In his undergraduate thesis, Foisy was the first to provide a precise statement of the three-dimensional double bubble conjecture, but he was unable to prove it.[10]

A proof for the restricted case of the double bubble conjecture, for two equal volumes, was announced by Joel Hass and Roger Schlafly in 1995, and published in 2000.[11][12] The proof of the full conjecture by Hutchings, Morgan, Ritoré, and Ros was announced in 2000 and published in 2002.[6][10][13] After earlier work on the four-dimensional case,[14] the full generalization to higher dimensions was published by Reichardt in 2008,[7] and in 2014, Lawlor published an alternative proof of the double bubble theorem generalizing both to higher dimensions and to weighted forms of surface energy.[1] Variations of the problem considering other measures of the size of the enclosing surface, such as its Gaussian measure, have also been studied.[15]

A lemma of Brian White shows that the minimum area double bubble must be a surface of revolution. For, if not, one could use a similar argument to the ham sandwich theorem to find two orthogonal planes that bisect both volumes, replace surfaces in two of the four quadrants by the reflections of the surfaces in the other quadrants, and then smooth the singularities at the reflection planes, reducing the total area.[8] Based on this lemma, Michael Hutchings was able to restrict the possible shapes of non-standard optimal double bubbles, to consist of layers of toroidal tubes.[16]

Additionally, Hutchings showed that the number of toroids in a non-standard but minimizing double bubble could be bounded by a function of the two volumes. In particular, for two equal volumes, the only possible nonstandard double bubble consists of a single central bubble with a single toroid around its equator. Based on this simplification of the problem, Joel Hass and Roger Schlafly were able to reduce the proof of this case of the double bubble conjecture to a large computerized case analysis, taking 20 minutes on a 1995 personal computer.[8][12] The eventual proof of the full double bubble conjecture also uses Hutchings' method to reduce the problem to a finite case analysis, but it avoids the use of computer calculations, and instead works by showing that all possible nonstandard double bubbles are unstable: they can be perturbed by arbitrarily small amounts to produce another surface with lower area. The perturbations needed to prove this result are a carefully chosen set of rotations. Because a surface of minimum area exists, and none of the other candidate surfaces have minimum area, the minimum-area surface can only be the standard double bubble.[8][2]

Limiting shape of the curve-shortening flow for three regions, a degenerate planar double bubble with two infinite regions

John M. Sullivan has conjectured that, for any dimension ${\displaystyle d}$, the minimum enclosure of up to ${\displaystyle d+1}$ volumes (not necessarily equal) has the form of a stereographic projection of a simplex.[17] In particular, in this case, all boundaries between bubbles would be patches of spheres. The special case of this conjecture for three bubbles in two dimensions has been proven; in this case, the three bubbles are formed by six circular arcs and straight line segments, meeting in the same combinatorial pattern as the edges of a tetrahedron.[18] Frank Morgan called even the case of three volumes in three dimensions "inaccessible",[19] but in 2022 a proof was announced of the three-volume case in all dimensions, and of additional partial results in higher dimensions.[20][21] Numerical experiments have shown that for six or more volumes in three dimensions, some of the boundaries between bubbles may be non-spherical.[17]

For an infinite number of equal areas in the plane, the minimum-length set of curves separating these areas is the hexagonal tiling, familiar from its use by bees to form honeycombs, and its optimality (the honeycomb conjecture) was proven by T. C. Hales in 2001.[22] For the same problem in three dimensions, the optimal solution is not known; Lord Kelvin conjectured that it was given by a structure combinatorially equivalent to the bitruncated cubic honeycomb, but this conjecture was disproved by the discovery of the Weaire–Phelan structure, a partition of space into equal volume cells of two different shapes using a smaller average amount of surface area per cell.[23]

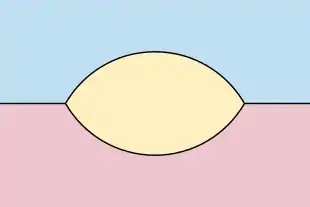
Researchers have also studied the dynamics of physical processes by which pairs of bubbles coalesce into a double bubble.[24][25] This topic relates to a more general topic in differential geometry of the dynamic behavior of curves and surfaces under different processes that change them continuously. For instance, the curve-shortening flow is a process in which curves in the plane move at a speed proportionally to their curvature. For two infinite regions separated by a line, with a third finite region between them, the curve-shortening flow on their boundaries (rescaled to preserve the area of the finite region) converges towards a limiting shape in the form of a degenerate double bubble: a vesica piscis along the line between the two unbounded regions.[26]

• Weisstein, Eric W., "Double Bubble", MathWorld