Double group

In magnetochemistry, the need for a double group arises in a very particular circumstance, namely, in the treatment of the paramagnetism of complexes of a metal ion in whose electronic structure there is a single electron (or its equivalent, a single vacancy) in a metal ion's d- or f- shell. This occurs, for example, with the elements copper and silver in the +2 oxidation state, where there is a single vacancy in a d-electron shell, with titanium(III) which has a single electron in the 3d shell and with cerium(III) which has a single electron in the 4f shell.

In group theory, the character ${\displaystyle \chi }$, for rotation of a molecular wavefunction for angular momentum by an angle α is given by

${\displaystyle \chi ^{J}(\alpha )={\frac {\sin(J+{1 \over 2})\alpha }{\sin {1 \over 2}\alpha }}}$

where ${\displaystyle J=L+S}$; angular momentum is the vector sum of orbital and spin angular momentum. This formula applies with most paramagnetic chemical compounds of transition metals and lanthanides. However, in a complex containing an atom with a single electron in the valence shell, the character, ${\displaystyle \chi ^{J}}$, for a rotation through an angle of ${\displaystyle 2\pi +\alpha }$ about an axis through that atom is equal to minus the character for a rotation through an angle of ${\displaystyle \alpha }$[3]

${\displaystyle \chi ^{J}(2\pi +\alpha )=-\chi ^{J}(\alpha )}$

The change of sign cannot be true for an identity operation in any point group. Therefore, a double group, in which rotation by ${\displaystyle 2\pi }$, is classified as being distinct from the identity operation, is used. A character table for the double group D'₄ is as follows. The new symmetry operations are shown in the second row of the table.

Character table: double group D'₄

D'4	E		C4	C43	C2	2C'2	2C''2
		R	C4R	C43R	C2R	2C'2R	2C''2R
A'1	1	1	1	1	1	1	1
A'2	1	1	1	1	1	-1	-1
B'1	1	1	-1	-1	1	1	-1
B'2	1	1	-1	-1	1	-1	1
E'1	2	-2	0	0	-2	0	0
E'2	2	-2	√2	-√2	0	0	0
E'3	2	-2	-√2	√2	0	0	0

The symmetry operations such as C₄ and C₄R belong to the same class but the column header is shown, for convenience, in two rows, rather than C₄, C₄R in a single row .

Character tables for the double groups T', O', T_d', D_3h', C_6v', D₆', D_2d', C_4v', D₄', C_3v', D₃', C_2v', D₂' and R(3)' are given in Salthouse and Ware.[4]

Applications

Sub-structure at the center of an octahedral complex

Structure of a square-planar complex ion such as [AgF₄]^2-

An atom or ion (red) held in a C₆₀ fullerene cage

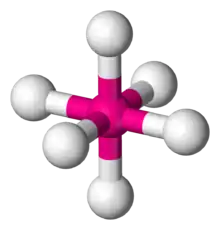
The need for a double group occurs, for example, in the treatment of magnetic properties of 6-coordinate complexes of copper(II). The electronic configuration of the central Cu²⁺ ion can be written as [Ar]3d⁹. It can be said that there is a single vacancy, or hole, in the copper 3d-electron shell, which can contain up to 10 electrons. The ion [Cu(H₂O)₆]²⁺ is a typical example of a compound with this characteristic.

(1) Six-coordinate complexes of the Cu(II) ion, with the generic formula [CuL₆]²⁺, are subject to the Jahn-Teller effect so that the symmetry is reduced from octahedral (point group O_h) to tetragonal (point group D_4h). Since d orbitals are centrosymmetric the related atomic term symbols can be classified in the subgroup D₄ .

(2) To a first approximation spin–orbit coupling can be ignored and the magnetic moment is then predicted to be 1.73 Bohr magnetons, the so-called spin-only value. However, for a more accurate prediction spin–orbit coupling must be taken into consideration. This means that the relevant quantum number is J, where J = L + S.

(3) When J is half-integer, the character for a rotation by an angle of α + 2π radians is equal to minus the character for rotation by an angle α. This cannot be true for an identity in a point group. Consequently, a group must be used in which rotations by α + 2π are classed as symmetry operations distinct from rotations by an angle α. This group is known as the double group, D₄'.

With species such as the square-planar complex of the silver(II) ion [AgF₄]^2- the relevant double group is also D₄'; deviations from the spin-only value are greater as the magnitude of spin–orbit coupling is greater for silver(II) than for copper(II).[5]

A double group is also used for some compounds of titanium in the +3 oxidation state. Titanium(III) has a single electron in the 3d shell; the magnetic moments of its complexes have been found to lie in the range 1.63 - 1.81 B.M. at room temperature.[6] The double group O' is used to classify their electronic states.

The cerium(III) ion, Ce³⁺, has a single electron in the 4f shell. The magnetic properties of octahedral complexes of this ion are treated using the double group O'.

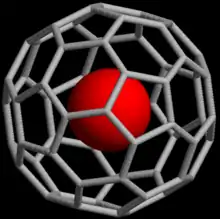
When a cerium(III) ion is encapsulated in a C₆₀ cage, the formula of the endohedral fullerene is written as {Ce³⁺@C₆₀^3-}. [7] The magnetic properties of the compound are treated using the icosahedral double group I²_h. [8]

Free radicals

Double groups may be used in connection with free radicals. This has been illustrated for the species CH₃F⁺ and CH₃BF₂⁺ which both contain a single unpaired electron.[9]

See also

• Molecular symmetry
• Point group
• Magnetochemistry

References

1. Cotton, F. Albert (1971). Chemical Applications of Group Theory. New York: Wiley. pp. 289–294, 376. ISBN 0-471-17570-6.
2. Tsukerblat, Boris S. (2006). Group Theory in Chemistry and Spectroscopy. Mineola, New York: Dover Publications Inc. pp. 245–253. ISBN 0-486-45035-X.
3. Lipson, R.H. "Spin-orbit coupling and double groups" (PDF).
4. Salthouse, J.A.; Ware, M.J. (1972). Point group character tables and related data. Cambridge: Cambridge University Press. pp. 55–57. ISBN 0-521-081394.
5. Foëx, D.; Gorter, C. J.; Smits, L.J. (1957). Constantes Sélectionées Diamagnetism et Paramagnetism. Paris: Masson et Cie.
6. Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. p. 971. ISBN 978-0-08-037941-8.
7. Chai, Yan; Guo, Ting; Jin, Changming; Haufler, Robert E.; Chibante, L. P. Felipe; Fure, Jan; Wang, Lihong; Alford, J. Michael; Smalley, Richard E. (1991). "Fullerenes with metals inside". The Journal of Physical Chemistry. 95 (20): 7564–7568. doi:10.1021/j100173a002.
8. Balasubramanian, K. (1996). "Double group of the icosahedral group (I_h) and its application to fullerenes". Chemical Physics Letters. 260 (3): 476–484. Bibcode:1996CPL...260..476B. doi:10.1016/0009-2614(96)00849-4.
9. Bunker, P.R. (1979), "The Spin Double Groups of Molecular Symmetry Groups", in Hinze, J. (ed.), The Permutation Group in Physics and Chemistry, Lecture Notes in Chemistry, vol. 12, Springer, pp. 38–56, doi:10.1007/978-3-642-93124-6_4, ISBN 978-3-540-09707-5

Further reading

Earnshaw, Alan (1968). Introduction to Magnetochemistry. Academic Press.

Figgis, Brian N.; Lewis, Jack (1960). "The magnetochemistry of complex compounds". In Lewis, J.; Wilkins, R.G. (eds.). Modern Coordination Chemistry. New York: Interscience. pp. 400–451.

Orchard, Anthony F. (2003). Magnetochemistry. Oxford Chemistry Primers. Oxford University Press. ISBN 0-19-879278-6.

Vulfson, Sergey G.; Arshinova, Rose P. (1998). Molecular Magnetochemistry. Taylor & Francis. ISBN 90-5699-535-9.