Euler's pump and turbine equation

A consequence of Newton's second law of mechanics is the conservation of the angular momentum (or the “moment of momentum”) which is fundamental to all turbomachines. Accordingly, the change of the angular momentum is equal to the sum of the external moments. The variation of angular momentum ${\displaystyle \rho \cdot Q\cdot r\cdot c_{u}}$ at inlet and outlet, an external torque ${\displaystyle M}$ and friction moments due to shear stresses ${\displaystyle M_{\tau }}$ act on an impeller or a diffuser.

Since no pressure forces are created on cylindrical surfaces in the circumferential direction, it is possible to write:

${\displaystyle \rho Q(c_{2u}r_{2}-c_{1u}r_{1})=M+M_{\tau }\,}$ (1.13)[2]

${\displaystyle c_{2u}=c_{2}\cos \alpha _{2}\,}$

${\displaystyle c_{1u}=c_{1}\cos \alpha _{1}.\,}$

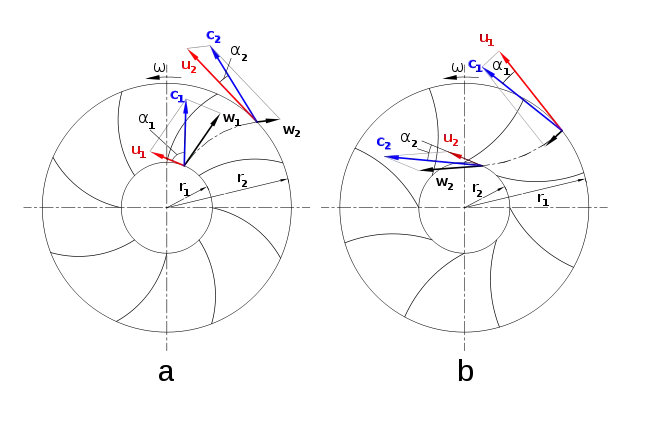
The color triangles formed by velocity vectors u,c and w are called velocity triangles and are helpful in explaining how pumps work.

${\displaystyle c_{1}\,}$ and ${\displaystyle c_{2}\,}$ are the absolute velocities of the fluid at the inlet and outlet respectively.

${\displaystyle w_{1}\,}$ and ${\displaystyle w_{2}\,}$ are the relative velocities of the fluid with respect to the blade at the inlet and outlet respectively.

${\displaystyle u_{1}\,}$ and ${\displaystyle u_{2}\,}$ are the velocities of the blade at the inlet and outlet respectively.

${\displaystyle \omega }$ is angular velocity.

Figures 'a' and 'b' show impellers with backward and forward-curved vanes respectively.

Based on Eq.(1.13), Euler developed the equation for the pressure head created by an impeller:

${\displaystyle Y_{th}=H_{t}\cdot g=c_{2u}u_{2}-c_{1u}u_{1}}$ (1)

${\displaystyle Y_{th}=1/2(u_{2}^{2}-u_{1}^{2}+w_{1}^{2}-w_{2}^{2}+c_{2}^{2}-c_{1}^{2})}$ (2)

Y_th : theoretical specific supply ; H_t  : theoretical head pressure  ; g : gravitational acceleration

For the case of a Pelton turbine the static component of the head is zero, hence the equation reduces to:

${\displaystyle H={1 \over {2g}}(V_{1}^{2}-V_{2}^{2}).\,}$

Euler’s pump and turbine equations can be used to predict the effect that changing the impeller geometry has on the head. Qualitative estimations can be made from the impeller geometry about the performance of the turbine/pump.

This equation can be written as rothalpy invariance:

${\displaystyle I=h_{0}-uc_{u}}$

where ${\displaystyle I}$ is constant across the rotor blade.

• Euler equations (fluid dynamics)
• List of topics named after Leonhard Euler
• Rothalpy