Exsymmedian

In Euclidean geometry, the exsymmedians are three lines associated with a triangle. More precisely, for a given triangle the exsymmedians are the tangent lines on the triangle's circumcircle through the three vertices of the triangle. The triangle formed by the three exsymmedians is the tangential triangle; its vertices, that is the three intersections of the exsymmedians, are called exsymmedian points.

  Reference triangle △ABC

  Circumcircle of △ABC

  Exsymmedians (e_a, e_b, e_c); intersect at the exsymmedian points (E_a, E_b, E_c)

  Symmedians (s_a, s_b, s_c)

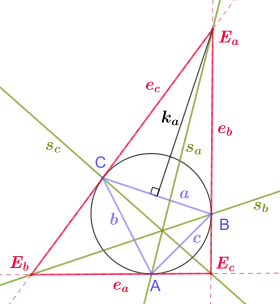
For a triangle △ABC with e_a, e_b, e_c being the exsymmedians and s_a, s_b, s_c being the symmedians through the vertices A, B, C, two exsymmedians and one symmedian intersect in a common point:

$${\displaystyle {\begin{aligned}E_{a}&=e_{b}\cap e_{c}\cap s_{a}\\E_{b}&=e_{a}\cap e_{c}\cap s_{b}\\E_{c}&=e_{a}\cap e_{b}\cap s_{c}\end{aligned}}}$$

The length of the perpendicular line segment connecting a triangle side with its associated exsymmedian point is proportional to that triangle side. Specifically the following formulas apply:

$${\displaystyle {\begin{aligned}k_{a}&=a\cdot {\frac {2\triangle }{c^{2}+b^{2}-a^{2}}}\\[6pt]k_{b}&=b\cdot {\frac {2\triangle }{c^{2}+a^{2}-b^{2}}}\\[6pt]k_{c}&=c\cdot {\frac {2\triangle }{a^{2}+b^{2}-c^{2}}}\end{aligned}}}$$

Here △ denotes the area of the triangle △ABC, and k_a, k_b, k_c denote the perpendicular line segments connecting the triangle sides a, b, c with the exsymmedian points E_a, E_b, E_c.