Extended discrete element method
The extended discrete element method (XDEM) is a numerical technique that extends the dynamics of granular material or particles as described through the classical discrete element method (DEM) (Cundall[1] and Allen[2]) by additional properties such as the thermodynamic state, stress/strain or electro-magnetic field for each particle. Contrary to a continuum mechanics concept, the XDEM aims at resolving the particulate phase with its various processes attached to the particles. While the discrete element method predicts position and orientation in space and time for each particle, the extended discrete element method additionally estimates properties such as internal temperature and/or species distribution or mechanical impact with structures.
History
Molecular dynamics developed in the late 1950s by Alder et al.[3] and early 1960s by Rahman[4] may be regarded as a first step toward the extended discrete element method, although the forces due to collisions between particles were replaced by energy potentials e.g. Lennard-Jones potentials of molecules and atoms as long range forces to determine interaction.
Similarly, the fluid dynamic interaction of particles suspended in a flow were investigated. The drag forces exerted on the particles by the relative velocity by them and the flow were treated as additional forces acting on the particles. Therefore, these multiphase flow phenomena including a solid e.g.~particulate and a gaseous or fluid phase resolve the particulate phase by discrete methods, while gas or liquid flow is described by continuous methods, and therefore, is labelled the combined continuum and discrete model (CCDM) as applied by Kawaguchi et al.,[5] Hoomans,[6] Xu 1997[7] and Xu 1998.[8] Due to a discrete description of the solid phase, constitutive relations are omitted, and therefore, leads to a better understanding of the fundamentals. This was also concluded by Zhu 2007 et al.[9] and Zhu 2008 et al.[10] during a review on particulate flows modelled with the CCDM approach. It has seen a mayor development in last two decades and describes motion of the solid phase by the Discrete Element Method (DEM) on an individual particle scale and the remaining phases are treated by the Navier-Stokes equations. Thus, the method is recognized as an effective tool to investigate into the interaction between a particulate and fluid phase as reviewed by Yu and Xu,[11] Feng and Yu [12] and Deen et al.[13] Based on the CCDM methodology the characteristics of spouted and fluidised beds are predicted by Gryczka et al.[14]
The theoretical foundation for the XDEM was developed in 1999 by Peters,[15] who described incineration of a wooden moving bed on a forward acting grate.[16] The concept was later also employed by Sismsek et al.[17] to predict the furnace process of a grate firing system. Applications to the complex processes of a blast furnace have been attempted by Shungo et al.[18] Numerical simulation of fluid injection into a gaseous environment nowadays is adopted by a large number of CFD-codes such as Simcenter STAR-CCM+, Ansys and AVL-Fire. Droplets of a spray are treated by a zero-dimensional approach to account for heat and mass transfer to the fluid phase.
Methodology

Many engineering problems exist that include continuous and discrete phases, and those problems cannot be simulated accurately by continuous or discrete approaches. XDEM provides a solution for some of those engineering applications.
Although research and development of numerical methods in each domains of discrete and continuous solvers is still progressing, software tools are available. In order to couple discrete and continuous approaches, two major approaches are available:
- Monolithic approach: The equations describing multi-physics phenomena are solved simultaneously by a single solver producing a complete solution.
- Partitioned or staggered approach: The equations describing multi-physics phenomena are solved sequentially by appropriately tailored and distinct solvers with passing the results of one analysis as a load to the other.
The former approach requires a solver that handles all physical problems involved, therefore it requires a larger implementation effort. However, there exist scenarios for which it is difficult to arrange the coefficients of combined differential equations in one matrix.
The latter, partitioned, approach couples a number of solvers representing individual domains of physics offers advantages over a monolithic concept. It encompasses a larger degree of flexibility because it can use many solvers. Furthermore, it allows a more modular software development. However, partitioned simulations require stable and accurate coupling algorithms.
Within the staggered concept of XDEM, continuous fields are described by the solution the respective continuous (conservation) equations. Properties of individual particles such as temperature are also resolved by solving respective conservation equations that yield both a spatial and temporal internal distribution of relevant variables. Major conservation principles with their equations and variables to be solved for and that are employed to an individual particle within XDEM are listed in the following table.
| Conservation law | Equation | Variable |
|---|---|---|
| Mass (compressible medium) | Continuity | Pressure/density |
| Linear Momentum | Navier-Stokes | Velocity |
| Energy | Energy | Temperature |
| Species mass | Species transport | Mass fractions |
| Charge, current | Maxwell | electric, magnetic field, electric displacement field |
The solution of these equations in principle defines a three-dimensional and transient field of the relevant variables such as temperature or species. However, the application of these conservation principles to a large number of particles usually restricts the resolution to at most one representative dimension and time due to CPU time consumption. Experimental evidence at least in reaction engineering supports the assumption of one-dimensionality as pointed out by Man and Byeong,[19] while the importance of a transient behaviour is stressed by Lee et al.[20]
Applications

Problems that involve both a continuous and a discrete phase are important in applications as diverse as pharmaceutical industry e.g.~drug production, agriculture food and processing industry, mining, construction and agricultural machinery, metals manufacturing, energy production and systems biology. Some predominant examples are coffee, corn flakes, nuts, coal, sand, renewable fuels e.g.~biomass for energy production and fertilizer.
Initially, such studies were limited to simple flow configurations as pointed out by Hoomans,[21] however, Chu and Yu[22] demonstrated that the method could be applied to a complex flow configuration consisting of a fluidized bed, conveyor belt and a cyclone. Similarly, Zhou et al.[23] applied the CCDM approach to the complex geometry of fuel-rich/lean burner for pulverised coal combustion in a plant and Chu et al.[24] modelled the complex flow of air, water, coal and magnetite particles of different sizes in a dense medium cyclone (DMC).
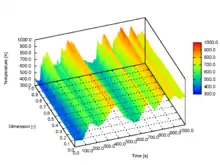
The CCDM approach has also been applied to fluidised beds as reviewed by Rowe and Nienow[25] and Feng and Yu[26] and applied by Feng and Yu[27] to the chaotic motion of particles of different sizes in a gas fluidized bed. Kafuia et al.[28] describe discrete particle-continuum fluid modelling of gas-solid fluidised beds. Further applications of XDEM include thermal conversion of biomass on a backward and forward acting grate. Heat transfer in thermal/reacting particulate systems was also solved and investigated, as comprehensively reviewed by Peng et al.[29] The deformation of a conveyor belt due to impacting granular material that is discharged over a chute represents an application in the field of stress/strain analysis.
 Distribution of particles' surface temperature on a backward acting grate. |
 Progress of pyrolysis of straw blades on a forward acting grate, on which straw is converted into charred material |
 Distribution of porosity inside the packed bed and particle temperature |
References
- Cundall, P. A.; Strack, O. D. L. (1979). "A discrete numerical model for granular assemblies". Geotechnique. 29: 47–65. doi:10.1680/geot.1979.29.1.47.
- Allen, M. P.; Tildesley, D. J. (1990). Computer Simulation of Liquids. Clarendon Press Oxford.
- Alder, B. J.; Wainwright, T. E. (1959). "Studies in Molecular Dynamics. I. General Method". J. Chem. Phys. 31 (2): 459–466. Bibcode:1959JChPh..31..459A. doi:10.1063/1.1730376.
- Rahman, A. (1964). "Correlations in the Motion of Atoms in Liquid Argon". Phys. Rev. 136 (2A): A405–A411. Bibcode:1964PhRv..136..405R. doi:10.1103/physrev.136.a405.
- Kawaguchi, T.; Tsuji, Y.; Tanaka, T. (1993). "Discrete particle simulation of two-dimensional fluidized bed". Powder Technol. 77: 79–87. doi:10.1016/0032-5910(93)85010-7.
- Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51: 99–118. CiteSeerX 10.1.1.470.6532. doi:10.1016/0009-2509(95)00271-5. S2CID 17460834.
- Xu, B. H.; Yu, A. B. (1997). "Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics". Chemical Engineering Science. 52 (16): 2785–2809. doi:10.1016/s0009-2509(97)00081-x.
- Xu, B. H.; Yu, A. B. (1998). "Comments on the paper numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics". Chemical Engineering Science. 53 (14): 2646–2647. doi:10.1016/s0009-2509(98)00086-4.
- Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2007). "Discrete particle simulation of particulate systems: Theoretical developments". Chemical Engineering Science. 62 (13): 3378–3396. doi:10.1016/j.ces.2006.12.089.
- Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2008). "Discrete particle simulation of particulate systems: A review of major applications and findings". Chemical Engineering Science. 63 (23): 5728–5770. doi:10.1016/j.ces.2008.08.006.
- Xu, B. H.; Yu, A. B. (2003). "Particle-scale modelling of gas-solid flow in fluidisation". Journal of Chemical Technology and Biotechnology. 78 (2–3): 111–121. doi:10.1002/jctb.788.
- Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43 (26): 8378–8390. doi:10.1021/ie049387v.
- Deen, N. G.; Annaland, M. V. S.; Van Der Hoef, M. A.; Kuipers, J. A. M. (2007). "Review of discrete particle modeling of fluidized beds". Chemical Engineering Science. 62 (1–2): 28–44. doi:10.1016/j.ces.2006.08.014.
- Gryczka, O.; Heinrich, S.; Deen, N. S.; van Sint Annaland, M.; Kuipers, J. A. M.; Mörl, M. (2009). "CFD modeling of a prismatic spouted bed with two adjustable gas inlets". Canadian Journal of Chemical Engineering. 87 (2): 318–328. CiteSeerX 10.1.1.335.4108. doi:10.1002/cjce.20143.
- Peters, B. (1999). "Classification of combustion regimes in a packed bed based on the relevant time and length scales". Combustion and Flame. 116 (1–2): 297–301. doi:10.1016/s0010-2180(98)00048-0.
- Peters, B. (2002). "Measurements and application of a discrete particle model (DPM) to simulate combustion of a packed bed of individual fuel particles". Combustion and Flame. 131 (1–2): 132–146. doi:10.1016/s0010-2180(02)00393-0.
- Simsek, E.; Brosch, B.; Wirtz, S.; Scherer, V.; Kröll, F. (2009). "Numerical simulation of grate firing systems using a coupled CFD/Discrete Element Method (DEM)". Powder Technology. 193 (3): 266–273. doi:10.1016/j.powtec.2009.03.011.
- Natsui, Shungo; Ueda, Shigeru; Fan, Zhengyun; Andersson, Nils; Kano, Junya; Inoue, Ryo; Ariyama, Tatsuro (2010). "Characteristics of solid flow and stress distribution including asymmetric phenomena in blast furnace analyzed by discrete element method". ISIJ International. 50 (2): 207–214. doi:10.2355/isijinternational.50.207.
- Man, Y. H.; Byeong, R. C. (1994). "A numerical study on the combustion of a single carbon particle entrained in a steady flow". Combustion and Flame. 97: 1–16. doi:10.1016/0010-2180(94)90112-0.
- Lee, J. C.; Yetter, R. A.; Dryer, F. L. (1996). "Numerical simulation of laser ignition of an isolated carbon particle in quiescent environment". Combustion and Flame. 105 (4): 591–599. doi:10.1016/0010-2180(96)00221-0.
- Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51: 99–118. CiteSeerX 10.1.1.470.6532. doi:10.1016/0009-2509(95)00271-5. S2CID 17460834.
- Chu, K. W.; Yu, A. B. (2008). "Numerical simulation of complex particle-fluid flows". Powder Technology. 179 (3): 104–114. doi:10.1016/j.powtec.2007.06.017.
- Zhou, H.; Mo, G.; Zhao, J.; Cen, K. (2011). "DEM-CFD simulation of the particle dispersion in a gas-solid two-phase flow for a fuel-rich/lean burner". Fuel. 90 (4): 1584–1590. doi:10.1016/j.fuel.2010.10.017.
- Chu, K. W.; Wang, B.; Yu, A. B.; Vince, A.; Barnett, G. D.; Barnett, P. J. (2009). "CFD-DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone". Minerals Engineering. 22 (11): 893–909. doi:10.1016/j.mineng.2009.04.008.
- Rowe, P. N.; Nienow, A. W. (1976). "Particle mixing and segregation in gas fluidized beds: A review". Powder Technology. 15 (2): 141–147. doi:10.1016/0032-5910(76)80042-3.
- Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43 (26): 8378–8390. doi:10.1021/ie049387v.
- Feng, Y. Q.; Yu, A. B. (2008). "An analysis of the chaotic motion of particles of different sizes in a gas fluidized bed". Particuology. 6 (6): 549–556. doi:10.1016/j.partic.2008.07.011.
- Kafuia, K. D.; Thornton, C.; Adams, M. J. (2002). "Discrete particle-continuum fluid modelling of gas-solid fluidised beds". Chemical Engineering Science. 57 (13): 2395–2410. doi:10.1016/s0009-2509(02)00140-9.
- Peng, Z.; Doroodchi, E.; Moghtaderi, B. (2020). "Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development". Progress in Energy and Combustion Science. 79, 100847: 100847. doi:10.1016/j.pecs.2020.100847. S2CID 218967044.