Instability

In the theory of dynamical systems, a state variable in a system is said to be unstable if it evolves without bounds. A system itself is said to be unstable if at least one of its state variables is unstable.

In continuous time control theory, a system is unstable if any of the roots of its characteristic equation has real part greater than zero (or if zero is a repeated root). This is equivalent to any of the eigenvalues of the state matrix having either real part greater than zero, or, for the eigenvalues on the imaginary axis, the algebraic multiplicity being larger than the geometric multiplicity. The equivalent condition in discrete time is that at least one of the eigenvalues is greater than 1 in absolute value, or that two or more eigenvalues are equal and of unit absolute value.

• Buckling
• Elastic instability
• Drucker stability of a nonlinear constitutive model
• Biot instability (surface wrinkling in elastomers)
• Baroclinic instability [2]

Hydrodynamics simulation of the Rayleigh–Taylor instability[3]

Unstable flow structure generated from the collision of two impinging jets.

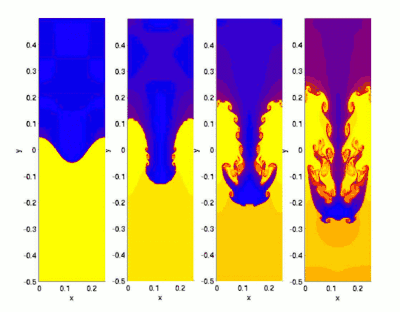
Fluid instabilities occur in liquids, gases and plasmas, and are often characterized by the shape that form; they are studied in fluid dynamics and magnetohydrodynamics. Fluid instabilities include:

• Ballooning instability (some analogy to the Rayleigh–Taylor instability); found in the magnetosphere
• Atmospheric instability
  • Hydrodynamic instability or dynamic instability (atmospheric dynamics)
    • Inertial instability; baroclinic instability; symmetric instability, conditional symmetric or convective symmetric instability; barotropic instability; Helmholtz or shearing instability; rotational instability
  • Hydrostatic instability or static instability/vertical instability (parcel instability), thermodynamic instability (atmospheric thermodynamics)
    • Conditional or static instability, buoyant instability, latent instability, nonlocal static instability, conditional-symmetric instability; convective, potential, or thermal instability, convective instability of the first and second kind; absolute or mechanical instability
• Bénard instability
• Drift mirror instability
• Kelvin–Helmholtz instability (similar, but different from the diocotron instability in plasmas)
• Rayleigh–Taylor instability
• Plateau-Rayleigh instability (similar to the Rayleigh–Taylor instability)
• Richtmyer-Meshkov instability (similar to the Rayleigh–Taylor instability)
• Shock Wave Instability
• Benjamin-Feir Instability (also known as modulational instability)

Plasma instabilities can be divided into two general groups (1) hydrodynamic instabilities (2) kinetic instabilities. Plasma instabilities are also categorised into different modes – see this paragraph in plasma stability.

Galaxies and star clusters can be unstable, if small perturbations in the gravitational potential cause changes in the density that reinforce the original perturbation. Such instabilities usually require that the motions of stars be highly correlated, so that the perturbation is not "smeared out" by random motions. After the instability has run its course, the system is typically "hotter" (the motions are more random) or rounder than before. Instabilities in stellar systems include:

• Bar instability of rapidly rotating disks
• Jeans instability
• Firehose instability[4]
• Gravothermal instability[5]
• Radial-orbit instability
• Various instabilities in cold rotating disks

The most common residual disability after any sprain in the body is instability. Mechanical instability includes insufficient stabilizing structures and mobility that exceed the physiological limits. Functional instability involves recurrent sprains or a feeling of giving way of the injured joint.[6] Injuries cause proprioceptive deficits and impaired postural control in the joint. Individuals with muscular weakness, occult instability, and decreased postural control are more susceptible to injury than those with better postural control. Instability leads to an increase in postural sway, the measurement of the time and distance a subject spends away from an ideal center of pressure. The measurement of a subject's postural sway can be calculated through testing center of pressure (CoP), which is defined as the vertical projection of center of mass on the ground. Investigators have theorized that if injuries to joints cause deafferentation, the interruption of sensory nerve fibers, and functional instability, then a subject's postural sway should be altered.[7] Joint stability can be enhanced by the use of an external support system, like a brace, to alter body mechanics. The mechanical support provided by a brace provides cutaneous afferent feedback in maintaining postural control and increasing stability.

• eFluids Fluid Flow Image Gallery