Free field (acoustics)

The lack of reflections in a free field means that any sound in the field is entirely determined by a listener or microphone because it is received through the direct sound of the sound source. This makes the open field a direct sound field.[3] In a free field, sound is attenuated with increased distance according to the inverse-square law.[1]

In nature, free field conditions occur only when sound reflections from the floor can be ignored, e.g. in new snow in a field, or approximately at good sound-absorbing floors (deciduous, dry sand, etc.) Free field conditions can be artificially produced in anechoic chambers. In particular, free field conditions play a major role in acoustic measurements and sound perception experiments as results are isolated from room reflections.

With voice and sound recordings, one often seeks a condition free from sound reflections similar to a free field, even when during post-processing specifically desired spatial impression will be added, because this is not distorted by any sound reflections of the recording room.

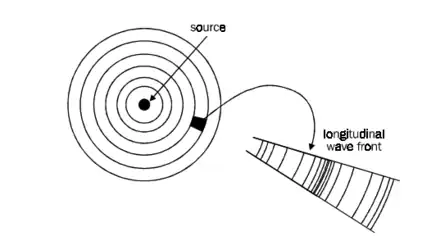
In the simple example shown in Figure 1, a singular sound source emits sound evenly and spherically with no obstructions.[1]

Figure 1.

The sound intensity and pressure level of any point in a free field is calculated below, where r (in meters) is the distance from the source and "where ρ and c are the air density and speed of sound respectively.[1]

${\displaystyle p^{2}=\rho cI=\rho cW/4\pi r^{2}}$ [1]

To calculate for air pressure, the equation can be written differently:[1]

${\displaystyle L_{p}=L_{w}+10\log _{10}(\rho c/400)-10\log _{10}(4\pi r^{2})}$ [1]

In order to simplify this equation we can remove elements:[1]

${\displaystyle L_{p}=L_{w}-10\log _{10}(4\pi r^{2})}$ [1]

Measuring the sound pressure level at a reference distance (Rm) from the source allows us measure another distance (r) more easily than other methods:[1]

${\displaystyle {\displaystyle L_{p}=L_{m}-20\log _{10}(r/r_{m})}}$ [1]

This means that as the distance from the sources doubles, the noise level decreases by 6 dB for each doubling. However if the sound field is not truly free of reflections, a directivity factor Q will help "characterise the directional sound radiation properties of a source."[1]

• Line array § Theory