Fundamental theorem on homomorphisms
In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, or the first isomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism.
The homomorphism theorem is used to prove the isomorphism theorems.
Group theoretic version

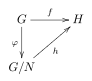
Given two groups G and H and a group homomorphism f : G → H, let N be a normal subgroup in G and φ the natural surjective homomorphism G → G/N (where G/N is the quotient group of G by N). If N is a subset of ker(f) then there exists a unique homomorphism h: G/N → H such that f = h∘φ.
In other words, the natural projection φ is universal among homomorphisms on G that map N to the identity element.
The situation is described by the following commutative diagram:
h is injective if and only if N = ker(f). Therefore, by setting N = ker(f) we immediately get the first isomorphism theorem.
We can write the statement of the fundamental theorem on homomorphisms of groups as "every homomorphic image of a group is isomorphic to a quotient group".
Proof
The proof follows from two basic facts about homomorphisms, namely their preservation of the group operation, and their mapping of the identity element to the identity element. We need to show that if is a homomorphism of groups, then: is a subgroup of . is isomorphic to .
Proof of 1
The operation that is preserved by is the group operation. If , then there exist elements such that and . For these and , we have (since preserves the group operation), and thus, the closure property is satisfied in . The identity element is also in because maps the identity element of to it. Since every element in has an inverse such that (because preserves the inverse property as well), we have an inverse for each element in , therefore, is a subgroup of .
Proof of 2
Construct a map by . This map is well-defined, as if , then and so which gives . This map is an isomorphism. is surjective onto by definition. To show injectiveness, if , then , which implies so .
Finally,
hence preserves the group operation. Hence is an isomorphism between and , which completes the proof.
Other versions
Similar theorems are valid for monoids, vector spaces, modules, and rings.
See also
References
- Beachy, John A. (1999), "Theorem 1.2.7 (The fundamental homomorphism theorem)", Introductory Lectures on Rings and Modules, London Mathematical Society Student Texts, vol. 47, Cambridge University Press, p. 27, ISBN 9780521644075.
- Grove, Larry C. (2012), "Theorem 1.11 (The Fundamental Homomorphism Theorem)", Algebra, Dover Books on Mathematics, Courier Corporation, p. 11, ISBN 9780486142135.
- Jacobson, Nathan (2012), "Fundamental theorem on homomorphisms of Ω-algebras", Basic Algebra II, Dover Books on Mathematics (2nd ed.), Courier Corporation, p. 62, ISBN 9780486135212.
- Rose, John S. (1994), "3.24 Fundamental theorem on homomorphisms", A course on Group Theory [reprint of the 1978 original], Dover Publications, Inc., New York, pp. 44–45, ISBN 0-486-68194-7, MR 1298629.