Gömböc

If analyzed quantitatively in terms of flatness and thickness, the discovered mono-monostatic bodies are the most sphere-like, apart from the sphere itself. Because of this, the first physical example was named gömböc, a diminutive form of gömb ("sphere" in Hungarian).

When a roly-poly toy is pushed, the height of the center of mass rises from the green line to the orange line, and the center of mass is no longer over the point of contact with the ground.

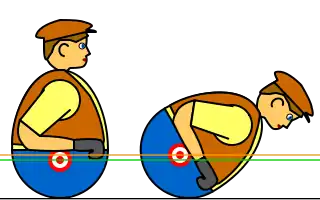
In geometry, a body with a single stable resting position is called monostatic, and the term mono-monostatic has been coined to describe a body which additionally has only one unstable point of balance. (The previously known monostatic polyhedron does not qualify, as it has several unstable equilibria.) A sphere weighted so that its center of mass is shifted from the geometrical center is mono-monostatic. However, it is inhomogeneous; that is, its material density varies across its body. Another example of an inhomogeneous mono-monostatic body is the Comeback Kid, Weeble or roly-poly toy (see left figure). At equilibrium, the center of mass and the contact point are on the line perpendicular to the ground. When the toy is pushed, its center of mass rises and shifts away from that line. This produces a righting moment, which returns the toy to the equilibrium position.

The above examples of mono-monostatic objects are necessarily inhomogeneous. The question of whether it is possible to construct a three-dimensional body which is mono-monostatic but also homogeneous and convex was raised by Russian mathematician Vladimir Arnold in 1995. Being convex is essential as it is trivial to construct a mono-monostatic non-convex body: an example would be a ball with a cavity inside it. It was already well known, from a geometrical and topological generalization of the classical four-vertex theorem, that a plane curve has at least four extrema of curvature, specifically, at least two local maxima and at least two local minima (see right figure), meaning that a (convex) mono-monostatic object does not exist in two dimensions. Whereas a common anticipation was that a three-dimensional body should also have at least four extrema, Arnold conjectured that this number could be smaller.[5]

An ellipse (red) and its evolute (blue), showing the four vertices of the curve. Each vertex corresponds to a cusp on the evolute.

The characteristic shape of the gömböc

The problem was solved in 2006 by Gábor Domokos and Péter Várkonyi. Domokos met Arnold in 1995 at a major mathematics conference in Hamburg, where Arnold presented a plenary talk illustrating that most geometrical problems have four solutions or extremal points. In a personal discussion, however, Arnold questioned whether four is a requirement for mono-monostatic bodies and encouraged Domokos to seek examples with fewer equilibria.[6]

The rigorous proof of the solution can be found in references of their work.[5] The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique. Such bodies are hard to visualize, describe or identify. Their form is dissimilar to any typical representative of any other equilibrium geometrical class. They should have minimal "flatness" and, to avoid having two unstable equilibria, must also have minimal "thinness". They are the only non-degenerate objects having simultaneously minimal flatness and thinness. The shape of those bodies is susceptible to small variation, outside which it is no longer mono-monostatic. For example, the first solution of Domokos and Várkonyi closely resembled a sphere, with a shape deviation of only 10⁻⁵. It was dismissed as it was tough to test experimentally.[7] The gömböc, as the first physical example, is less sensitive; yet it has a shape tolerance of 10⁻³, that is 0.1 mm for a 10 cm size.

Domokos developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points.[8] In one experiment, Domokos and his wife tested 2000 pebbles collected on the beaches of the Greek island of Rhodes and found not a single mono-monostatic body among them, illustrating the difficulty of finding or constructing such a body.[5][7]

The solution of Domokos and Várkonyi has curved edges and resembles a sphere with a squashed top. In the top figure, it rests in its stable equilibrium. Its unstable equilibrium position is obtained by rotating the figure 180° about a horizontal axis. Theoretically, it will rest there, but the smallest perturbation will bring it back to the stable point. All mono-monostatic shapes (including the gömböc shape) have sphere-like properties. In particular, its flatness and thinness are minimal, and this is the only type of nondegenerate object with this property.[5] Domokos and Várkonyi are interested in finding a polyhedral solution with a surface consisting of a minimal number of flat planes. There is a prize[3] to anyone who finds the respective minimal numbers of F, E, and V faces, edges and vertices for such a polyhedron, which amounts to $10,000 divided by the number C = F + E + V − 2, which is called the mechanical complexity of mono-monostatic polyhedra. It has been proved that one can approximate a curvilinear mono-monostatic shape with a finite number of discrete surfaces;[9] however, they estimate that it would take thousands of planes to achieve that. By offering this prize, they hope to stimulate finding a radically different solution from their own.[3]

The shape of the Indian star tortoise resembles a gömböc. This tortoise rolls easily to a right-side-up position without relying much on its limbs.

The Argentine snake-necked turtle is an example of a flat turtle, which relies on its long neck and legs to turn over when placed upside down.

The balancing properties of the gömböc are associated with the "righting response" ⁠— the ability to turn back when placed upside down⁠ ⁠— of shelled animals such as tortoises and beetles. These animals may become flipped over in a fight or predator attack, and so the righting response is crucial for survival. In order to right themselves, relatively flat animals (such as beetles) heavily rely on momentum and thrust developed by moving their limbs and wings. However, the limbs of many dome-shaped tortoises are too short to be of use in for righting.

Domokos and Várkonyi spent a year measuring tortoises in the Budapest Zoo, Hungarian Museum of Natural History and various pet shops in Budapest, digitizing and analyzing their shells, and attempting to "explain" their body shapes and functions from their geometry work published by the biology journal Proceedings of the Royal Society.[10] It was then immediately popularized in several science news reports, including the science journals Nature[2] and Science.[3] The reported model can be summarized as flat shells in tortoises are advantageous for swimming and digging. However, the sharp shell edges hinder the rolling. Those tortoises usually have long legs and necks and actively use them to push the ground to return to the normal position if placed upside down. On the contrary, "rounder" tortoises easily roll on their own; those have shorter limbs and use them little when recovering from lost balance. (Some limb movement would always be needed because of imperfect shell shape, ground conditions, etc.) Round shells also resist better the crushing jaws of a predator and are better for thermal regulation.[1][2][3]

In the fall of 2020, the Korzo Theatre in The Hague and the Theatre Municipal in Biarritz presented the solo dance production "Gömböc" [11] by French choreographer Antonin Comestaz.[12]

A 2021 solo exhibition of conceptual artist Ryan Gander evolved around the theme of self-righting and featured seven large gömböc shapes gradually covered by black volcanic sand.[13]

For their discovery, Domokos and Várkonyi were decorated with the Knight's Cross of the Republic of Hungary.[14] The New York Times Magazine selected the gömböc as one of the 70 most interesting ideas of the year 2007.[15]

The Stamp News website[16] shows Hungary's new stamps issued on 30 April 2010, which illustrate a gömböc in different positions. The stamp booklets are arranged so that the gömböc appears to come to life when the booklet is flipped. The stamps were issued in association with the gömböc on display at the World Expo 2010 (1 May to 31 October). This was also covered by the Linn's Stamp News magazine.[17]

• Instability
• Monostatic polytope
• Self-righting watercraft

• Non-technical description of development, with short video
• Expo 2010 presentation of a gömböc shape, with photos