Data model (GIS)
A geographic data model, geospatial data model, or simply data model in the context of geographic information systems, is a mathematical and digital structure for representing phenomena over the Earth. Generally, such data models represent various aspects of these phenomena by means of geographic data, including spatial locations, attributes, change over time, and identity. For example, the vector data model represents geography as collections of points, lines, and polygons, and the raster data model represent geography as cell matrices that store numeric values.[1] Data models are implemented throughout the GIS ecosystem, including the software tools for data management and spatial analysis, data stored in a variety of GIS file formats, specifications and standards, and specific designs for GIS installations.
While the unique nature of spatial information has led to its own set of model structures, much of the process of data modeling is similar to the rest of information technology, including the progression from conceptual models to logical models to physical models, and the difference between generic models and application-specific designs.
History
The earliest computer systems that represented geographic phenomena were quantitative analysis models developed during the quantitative revolution in geography in the 1950s and 1960s; these could not be called a geographic information system because they did not attempt to store geographic data in a consistent permanent structure, but were usually statistical or mathematical models. The first true GIS software modeled spatial information using data models that would come to be known as raster or vector:
- SYMAP (by Howard Fisher, Harvard Laboratory for Computer Graphics and Spatial Analysis, developed 1963–1967) produced raster maps, although data was usually entered as vector-like region outlines or sample points then interpolated into a raster structure for output.[2] The GRID package, developed at the lab in 1969 by David Sinton, was based on SYMAP but was more focused on the permanent storage and analysis of gridded data, thus becoming perhaps the first general purpose raster GIS software.
- The Canadian Geographic Information System (by Roger Tomlinson, Canada Land Inventory, developed 1963–1968) stored natural resource data as "faces" (vector polygons), although these were typically derived from raster scans of paper maps.[3]
- Dual Independent Map Encoding (DIME, US Census Bureau, 1967) was perhaps the first robust vector data model incorporating network and polygon topology and attributes sufficient to allow address geocoding.[4]
- Like the CGIS, early GIS installations in the United States were often focused on inventories of land use and natural resources, including the Minnesota Land Management Information System (MLMIS, 1969), the Land Use and Natural Resources Inventory of New York (LUNR, 1970), and the Oak Ridge Regional Modelling Information System (ORRMIS, 1973). Unlike CGIS, these were all raster systems inspired by SYMAP, although the MLMIS was based on subsections of the Public Land Survey System, which is not a perfect regular grid.[5]
Most first-generation GIS were custom-built for specific needs, with data models designed to be stored and processed most efficiently using the technology limitations of the day (especially punched cards and limited mainframe processing time). During the 1970s, the early systems had produced sufficient results to compare them and evaluate the effectiveness of their underlying data models.[6] This led to efforts at the Harvard Lab and elsewhere focused on developing a new generation of generic data models, such as the POLYVRT topological vector model that would form the basis for commercial software and data such as the Esri Coverage.[7]
As commercial off-the-shelf GIS software, GIS installations, and GIS data proliferated in the 1980s, scholars began to look for conceptual models of geographic phenomena that seemed to underlay the common data models, trying to discover why the raster and vector data models seemed to make common sense, and how they measured and represented the real world.[8] This was one of the primary threads that formed the subdiscipline of geographic information science in the early 1990s.
Further developments in GIS data modeling in the 1990s were driven by rapid increases in both the GIS user base and computing capability. Major trends included 1) the development of extensions to the traditional data models to handle more complex needs such as time, three-dimensional structures, uncertainty, and multimedia; and 2) the need to efficiently manage exponentially increasing volumes of spatial data with enterprise needs for multiuser access and security. These trends eventually culminated in the emergence of spatial databases incorporated into relational databases and object-relational databases.
Types of data models
Because the world is much more complex than can be represented in a computer, all geospatial data are incomplete approximations of the world.[9] Thus, most geospatial data models encode some form of strategy for collecting a finite sample of an often infinite domain, and a structure to organize the sample in such a way as to enable interpolation of the nature of the unsampled portion. For example, a building consists of an infinite number of points in space; a vector polygon represents it with a few ordered points, which are connected into a closed outline by straight lines and assuming all interior points are part of the building; furthermore, a "height" attribute may be the only representation of its three-dimensional volume.
The process of designing geospatial data models is similar to data modeling in general, at least in its overall pattern. For example, it can be segmented into three distinct levels of model abstraction:[10]
- Conceptual data model, a high-level specification of how information is organized in the mind and in enterprise processes, without regard to the restrictions of GIS and other computer systems. It is common to develop and represent a conceptual model visually using tools such as an entity-relationship model.
- Logical data model, a broad strategy for how to represent the conceptual model in the computer, sometimes novel but often within the framework of existing software, hardware, and standards. The unified modeling language (UML), specifically the class diagram, is commonly used for visually developing logical and physical models.
- Physical data model, the detailed specification of how data will be structured in memory or in files.
Each of these models can be designed in one of two situations or scopes:
- A generic data model is intended to be employed in a wide variety applications, by discovering consistent patterns in the ways that society in general conceptualizes information and/or structures that work most efficiently in computers. For example, the field is a generic conceptual model of geographic phenomena, the relational database model and vector are generic logical models, while the shapefile format is a generic physical model. These models are typically implemented directly info software and GIS file formats. In the past, these models have been designed by academic researchers, by standards bodies such as the Open Geospatial Consortium, and by software vendors such as Esri. While academic and standard models are public (and sometimes open source), companies may choose to keep the details of their model a secret (as Esri attempted to do with the coverage and the file geodatabase) or to publish them openly (as Esri did with the shapefile).[11]
- A specific data model or GIS design is a specification of the data needed for a particular enterprise or project GIS application. It is generally created within the constraints of chosen generic data models, so that existing GIS software can be used. For example, a data model for a city would include a list of data layers to be included (e.g., roads, buildings, parcels, zoning), with each being specified with the type of generic spatial data model being used (e.g. raster or vector), choices of parameters such as coordinate system, and its attribute columns.
Conceptual spatial models
Generic geospatial conceptual models attempt to capture both the physical nature of geographic phenomena and how people think about them and work with them.[12] Contrary to the standard modeling process described above, the data models upon which GIS is built were not originally designed based on a general conceptual model of geographic phenomena, but were largely designed according to technical expediency, likely influenced by common sense conceptualizations that had not yet been documented.
That said, an early conceptual framework that was very influential in early GIS development was the recognition by Brian Berry and others that geographic information can be decomposed into the description of three very different aspects of each phenomenon: space, time, and attribute/property/theme.[13] As a further development in 1978, David Sinton presented a framework that characterized different strategies for measurement, data, and mapping as holding one of the three aspects constant, controlling a second, and measuring the third.[14]
During the 1980s and 1990s, a body of spatial information theories gradually emerged as a major subfield of geographic information science, incorporating elements of philosophy (especially ontology), linguistics, and sciences of spatial cognition. By the early 1990s, a basic dichotomy had emerged of two alternative ways of making sense of the world and its contents:
- An object (also called a feature or entity) is a distinct "thing," comprehended as a whole. It may be a visible, material object, such as a building or road, or an abstract entity such as a county or the market area of a retail store.
- A field is a property that varies over space, so that it potentially has a distinct measurable value at any location within its extent. It may be a physical, directly measurable characteristic of matter akin to the intensive properties of chemistry, such as temperature or density; or it may be an abstract concept defined via a mathematical model, such as the likelihood that a person living at each location will use a local park.[15]
These two conceptual models are not meant to represent different phenomena, but often are different ways of conceptualizing and describing the same phenomenon. For example, a lake is an object, but the temperature, clarity, and proportion of pollution of the water in the lake are each fields (the water itself may be considered as a third concept of a mass, but this is not as widely accepted as objects and fields).[16]
Vector data model
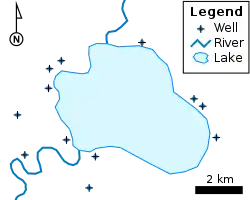
The vector logical model represents each geographic location or phenomenon by a geometric shape and a set of values for its attributes. Each geometric shape is represented using coordinate geometry, by a structured set of coordinates (x,y) in a geographic coordinate system, selected from a set of available geometric primitives, such as points, lines, and polygons.
Although there are dozens of vector file formats (i.e., physical data models) used in various GIS software, most conform to the Simple Feature Access (SFA) specification from the Open Geospatial Consortium (OGC). It was developed in the 1990s by finding common ground between existing vector models, and is now enshrined as ISO 19125, the reference standard for the vector data model. OGC-SFA includes the following vector geometric primitives:[17]
- Point: a single coordinate in two- or three-dimensional space. Many vector formats allow a single feature to consist of several isolated points and has a zero dimension. (a MultiPoint in OGC-SFA).
- Curve (alternatively called a polyline or linestring): a line includes an infinite number of points and has one-dimesnion, but it is represented by a finite ordered sample of points (called vertices), allowing for software to interpolate the intervening points. Traditionally, this was a linear interpolation (OGC-SFA calls this case a LineString), but some vector formats allow for curves (usually circular arcs or Bézier curves), or for a single feature to consist of multiple disjoint curves (a MultiCurve in OGC-SFA).
- Polygon: a region also includes an infinite number of points, so the vector model represents its boundary as a closed line (called a ring in OGC-SFA), allowing the software to interpolate the interior. GIS software distinguishes the interior and the exterior by requiring that the line be ordered counter-clockwise, so the interior is always on the left side of the boundary. In nearly every format, a polygon can have "holes" (e.g., an island in a lake) by including interior rings, each in clockwise order (so the interior is still on the left). As with lines, curved boundaries may be allowed; usually a single feature may include multiple polygons, which OGC-SFA collectively terms a surface.
- Text (alternatively called annotation): a minority of vector data formats, including the Esri geodatabase and Autodesk .dwg, support the storage of text in the database. An annotation is usually represented as a point or curve (the baseline) with a set of attributes giving the text content and design characteristics (font, size, spacing, etc.).
The geometric shape stored in a vector data set representing a phenomenon may or may not be of the same dimension as the real-world phenomenon itself.[18] It is common to represent a feature by a lower dimension than its real nature, based on the scale and purpose of the representation. For example, a city (a two-dimensional region) may be represented as a point, or a road (a three-dimensional structure) may be represented as a line. As long as the user is aware that the latter is a representation choice and a road is not really a line, this generalization can be useful for applications such as transport network analysis.
Based on this basic strategy of geometric shapes and attributes, vector data models use a variety of structures to collect these into a single data set (often called a layer), usually containing a set of related features (e.g., roads). These can be categorized into several approaches:
- The georelational data model was the basis for most early vector GIS software.[19] The geometric data and the attribute data are stored separately; this was originally because the geometric data required GIS-specific code to process it, but existing relational database software (RDBMS) could be used to manage the attributes. For example, Esri ARC/INFO (later ArcInfo) was originally composed of two separate programs: ARC was written by Esri for spatial management and analysis, while INFO was a licensed commercial RDBMS program. It was termed "georelational" because in keeping with the principles of relational databases, the geometry and attributes could be joined by matching each shape with a row in the table using a key, such as the row number or an ID number.[20]
- The spatial database (also called the object-based model[20]) first appeared in the 1990s. It also leverages the maturity of relational database management systems, especially for their ability to manage extremely large enterprise databases. Instead of storing geometric data separately, the spatial database defines a geometry data type, allowing the shapes to be stored in a column in the same table as the attributes, creating a single unified data set for each layer. Most RDBMS software (both commercial and open-source) have spatial extensions to enable the storage and query of geometric data, usually based on the Simple Features-SQL standard from the Open Geospatial Consortium.[21] Some non-database data formats also integrate geometric and attribute data for each object into a single structure, such as GeoJSON.
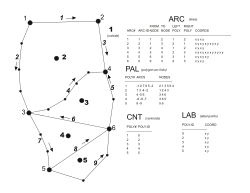
Vector data structures can also be classified by how they manage topological relationships between objects in a dataset:[22]
- A topological data model incorporates topological relationships as a core part of the model design.[18]: 46 The GBF/DIME format from the U.S. Census Bureau was probably the first topological data model; another early example was POLYVRT, developed at the Harvard Laboratory for Computer Graphics and Spatial Analysis in the 1970s, eventually evolving into the Esri ARC/INFO Coverage format.[7][19] In this structure, lines are broken at all intersection points; these nodes can then store topological information about which lines connect there. Polygons are not stored separately, but are defined as a set of lines that collectively close. Each line contains information about the polygons on its right and left, thus explicitly storing topological adjacency. This structure was designed to enable composite line-polygon structures (e.g., the census block), address geocoding, and transport network analysis. It also had the benefit of increased storage efficiency and reduced error, because the shared border of each pair of adjacent polygons was only digitized once. However, it is a fairly complicated data structure. Almost all topological data models are also geo-relational.
- A spaghetti data model does not include any information about topology (so-called because the individual strands in a bowl of spaghetti may overlap without connecting).[10]: 215 It was common in early GIS systems such as the Map Overlay and Statistical System (MOSS) as well as most recent data formats, such as the Esri shapefile, geography markup language (GML), and almost all spatial databases. In this model, each feature geometry is encoded separately from any others in the data set, regardless of whether they may be topologically related. For example, the shared boundary between two adjacent regions would be duplicated in each polygon shape. Despite the increased data volume and potential for error over topological data, this model has dominated GIS since 2000, largely due to its conceptual simplicity. Some GIS software has tools for validating topological integrity rules (e.g. not allowing polygons to overlap or have gaps) on spaghetti data to prevent and/or correct topological errors.
- A hybrid topological data model has the option of storing topological relationship information as a separate layer built on top of a spaghetti data set. An example is the network dataset within the Esri geodatabase.[23]
Vector data are commonly used to represent conceptual objects (e.g., trees, buildings, counties), but they can also represent fields. As an example of the latter, a temperature field could be represented by an irregular sample of points (e.g., weather stations), or by isotherms, a sample of lines of equal temperature.[10]: 89
Raster data model

The raster logical model represents a field using a tessellation of geographic space into a regularly spaced two-dimensional array of locations (each called a cell), with a single attribute value for each cell (or more than one value in a multi-band raster). Typically, each cell either represents a single central point sample (in which the measurement model for the entire raster is called a lattice) or it represents a summary (usually the mean) of the field variable over the square area (in which the model is called a grid).[9]: 86 The general data model is essentially the same as that used for images and other raster graphics, with the addition of capabilities for the geographic context. A small example follows:
| 6 | 7 | 10 | 9 | 8 | 6 | 7 | 8 |
| 6 | 8 | 9 | 10 | 8 | 7 | 7 | 7 |
| 7 | 8 | 9 | 10 | 9 | 8 | 7 | 6 |
| 8 | 8 | 9 | 11 | 10 | 9 | 9 | 7 |
| 8 | 9 | 10 | 11 | 11 | 10 | 10 | 8 |
| 9 | 9 | 10 | 10 | 11 | 10 | 9 | 8 |
| 7 | 8 | 9 | 10 | 10 | 9 | 9 | 7 |
| 7 | 7 | 8 | 9 | 8 | 8 | 7 | 6 |
To represent a raster grid in a computer file, it must be serialized into a single (one-dimensional) list of values. While there are various possible ordering schemes, the most commonly used is row-major, in which the cells in the first row, followed immediately by the cells in the second row, as follows:
6 7 10 9 8 6 7 8 6 8 9 10 8 7 7 7 7 8 9 10 9 8 7 6 8 8 9 11 10 9 9 7 . . .
To reconstruct the original grid, a header is required with general parameters for the grid. At the very least, it requires the number of rows in each column so it will know where to begin each new row, and the datatype of each value (i.e. the number of bits in each value before beginning the next value).[24]
While the raster model is closely tied to the field conceptual model, objects can also be represented in raster, essentially by transforming an object X into a discrete (Boolean) field of presence/absence of X. Alternatively, a layer of objects (usually polygons) could be transformed into a discrete field of object identifiers. In this case, some raster file formats allow a vector-like table of attributes to be joined to the raster by matching the ID values.[18] Raster representations of objects are often temporary, only created and used as part of a modelling procedure, rather than in a permanent data store.[20]: 135-137
To be useful in GIS, a raster file must be georeferenced to correspond to real world locations, as a raw raster can only express locations in terms of rows and columns. This is typically done with a set of metadata parameters, either in the file header (such as the GeoTIFF format) or in a sidecar file (such as a world file). At the very least, the georeferencing metadata must include the location of at least one cell in the chosen coordinate system and the resolution or cell size, the distance between each cell. A linear Affine transformation is the most common type of georeferencing, allowing rotation and rectangular cells.[18]: 171 More complex georeferencing schemes include polynomial and spline transformations.
Raster data sets can be very large, so image compression techniques are often used. Compression algorithms identify spatial patterns in the data, then transform the data into parameterized representations of the patterns, from which the original data can be reconstructed. In most GIS applications, lossless compression algorithms (e.g., Lempel-Ziv) are preferred over lossy ones (e.g., JPEG), because the complete original data are needed, not an interpolation.[10]
Extensions
Starting in the 1990s, as the original data models and GIS software matured, one of the primary foci of data modeling research was on developing extensions to the traditional models to handle more complex geographic information.
Spatiotemporal models
Time has always played an important role in analytical geography, dating at least back to Brian Berry's regional science matrix (1964) and the time geography of Torsten Hägerstrand (1970).[25][13] In the dawn of the GIScience era of the early 1990s, the work of Gail Langran opened the doors to research into methods of explicitly representing change over time in GIS data;[26] this led to many conceptual and data models emerging in the decades since.[27] Some forms of temporal data began to be supported in off-the-shelf GIS software by 2010.
Several common models for representing time in vector and raster GIS data include:[28]
- The snapshot model (also known as time-stamped layers), in which an entire dataset is tied to a particular valid time. That is, it is a "snapshot" of the world at that time.
- Time-stamped features, in which the dataset includes features valid at a variety of times, with each feature stamped by the time during which it was valid (i.e., by "start date" and "end date" columns in the attribute table.). Some GIS software, such as ArcGIS Pro, natively supports this model, with functionality including animation.
- Time-stamped boundaries, using the topological vector data model to decompose polygons into boundary segments, and stamping each segment by the time during which it was valid. This method was pioneered by the Great Britain Historical GIS.
- Time-stamped facts, in which each individual datum (including attribute values) can have its own time stamp, allowing for the attributes within a single feature to change over time, or for a single feature (with constant identity) to have different geometric shapes at different times.[29]
- Time as dimension, which treats time as another (3rd or 4th) spatial dimension, and using multidimensional vector or raster structures to create geometries incorporating time. Hägerstrand visualized his time geography this way, and some GIS models based on it use this approach. The NetCDF format supports managing temporal raster data as a dimension.[30]
Three-dimensional models
There are several approaches for representing three-dimensional map information, and for managing it in the data model. Some of these were developed specifically for GIS, while others have been adopted from 3D computer graphics or computer-aided drafting (CAD).
- Height fields (also known as "2 1/2 dimensional surfaces") model three-dimensional phenomena by a single functional surface, in which elevation is a function of two-dimensional location, allowing it to be represented using field techniques such as isolated points, contour lines, raster (the digital elevation model), and triangulated irregular networks.
- A polygon mesh (related to the mathematical polyhedron) is a logical extension of the vector data model, and is probably the 3-D model type most widely supported in GIS. A volumetric object is reduced to its outer surface, which is represented by a set of polygons (often triangles) that collectively completely enclose a volume.
- The voxel model is the logical extension of the raster data model, by tessellating three-dimensional space into cubes called voxels (a portmanteau of volume and pixel, the latter being itself a portmanteau). NetCDF is one of the most common data formats that supports 3-D cells.[30]
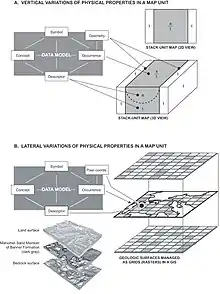
- Vector-based stack-unit maps depict the vertical succession of geologic units to a specified depth (here, the base of the block diagram). This mapping approach characterizes the vertical variations of physical properties in each 3-D map unit. In this example, an alluvial deposit (unit "a") overlies glacial till (unit "t"), and the stack-unit labeled "a/t" indicates that relationship, whereas the unit "t" indicates that glacial till extends down to the specified depth. In a manner similar to that shown in figure 11, the stack-unit's occurrence (the map unit's outcrop), geometry (the map unit's boundaries), and descriptors (the physical properties of the geologic units included in the stack-unit) are managed as they are for a typical 2-D geologic map.[31]
- Raster-based stacked surfaces depict the surface of each buried geologic unit, and can accommodate data on lateral variations of physical properties. In this example from Soller and others (1999),[32] the upper surface of each buried geologic unit was represented in raster format as an ArcInfo Grid file. The middle grid is the uppermost surface of an economically important aquifer, the Mahomet Sand, which fills a pre- and inter-glacial valley carved into the bedrock surface. Each geologic unit in raster format can be managed in the data model, in a manner not dissimilar from that shown for the stack-unit map. The Mahomet Sand is continuous in this area, and represents one occurrence of this unit in the data model. Each raster, or pixel, on the Mahomet Sand surface has a set of map coordinates that are recorded in a GIS (in the data model bin that is labeled "pixel coordinates", which is the raster corollary of the "geometry" bin for vector map data). Each pixel can have a unique set of descriptive information, such as surface elevation, unit thickness, lithology, transmissivity, etc.).
See also
References
- Wade, T. and Sommer, S. eds. A to Z GIS
- Robertson, J.C. (1967). "The Symap Programme for Computer Mapping". The Cartographic Journal. 4 (2): 108–113. doi:10.1179/caj.1967.4.2.108.
- Tomlinson, Roger (1968). "A Geographic Information System for Regional Planning". In Stewart, G.A. (ed.). Land Evaluation: Papers of a CSIRO Symposium. Macmillan of Australia. pp. 200–210.
- Cooke, Donald F. (1998). "Topology and TIGER: The Census Bureau's Contribution". In Foresman, Timothy W. (ed.). The History of Geographic Information Systems: Perspectives from the Pioneers. Prentice Hall. pp. 47–57.
- Tomlinson, Roger F.; Calkins, Hugh W.; Marble, Duane F. (1976). Computer handling of geographical data. UNESCO Press.
- Dueker, Kenneth J. (1972). "A Framework for Encoding Spatial Data". Geographical Analysis. 4 (1): 98–105. doi:10.1111/j.1538-4632.1972.tb00460.x.
- Peucker, Thomas K.; Chrisman, Nicholas (1975). "Cartographic Data Structures". The American Cartographer. 2 (1): 55–69. doi:10.1559/152304075784447289.
- Peuquet, Donna J. (1988). "Representations of Geographic Space: Toward a Conceptual Synthesis". Annals of the Association of American Geographers. 78 (3): 375–394. doi:10.1111/j.1467-8306.1988.tb00214.x.
- Huisman, Otto; de By, Rolf A. (2009). Principles of Geographic Information Systems (PDF). Enschede, The Netherlands: ITC. p. 64. Retrieved 1 November 2021.
- Longley, Paul A.; Goodchild, Michael F.; Maguire, David J.; Rhind, David W. (2011). Geographic Information Systems & Science (3rd ed.). Wiley. pp. 207–228.
- Esri. "ESRI Shapefile Technical Description" (PDF). Esri Technical Library. Retrieved 30 October 2021.
- Mennis, J.; Peuquet, D.J.; Qian, L. (2000). "A conceptual framework for incorporating cognitive principles into geographical database representation". International Journal of Geographical Information Science. 14 (6): 501–520. doi:10.1080/136588100415710. S2CID 7458359.
- Berry, Brian J.L. (1964). "Approaches to regional analysis: A synthesis". Annals of the Association of American Geographers. 54 (1): 2–11. doi:10.1111/j.1467-8306.1964.tb00469.x. S2CID 128770492.
- Sinton, David J. (1978). "The inherent structure of information as a constraint to analysis: Mapped thematic data as a case study". In Dutton, Geoff (ed.). Harvard Papers in GIS. Vol. 7. Harvard University.
- Peuquet, Donna J.; Smith, Barry; Brogaard, Berit, eds. (1997). The Ontology of Fields: Report of a Specialist Meeting Held under the Auspices of the Varenius Project (PDF).
- Plewe, Brandon (2019). "A Case for Geographic Masses". In Timpf, Sabine; Schlieder, Christoff; Kattenbeck, Marcus; Ludwig, Bernd (eds.). 14th International Conference on Spatial Information Theory (COSIT 2019). Schloss Dagstuhl-Leibniz-Zentrum für Informatik.
- Open Geospatial Consortium (2010). Simple feature access - Part 1: Common architecture. pp. 20–32.
- Bolstad, Paul (2019). GIS Fundamentals: A First Text on Geographic Information Systems (6th ed.). XanEdu. pp. 39–71.
- Morehouse, Scott (1985). "ARC/INFO: A geo-relational model for spatial information" (PDF). Proceedings of the International Symposium on Cartography and Computing (Auto-Carto VII): 388.
- Jensen, John R.; Jensen, Ryan R. (2013). "5: Spatial Data Models and Databases". Introductory Geographic Information Systems. Pearson. pp. 125–147.
- Open Geospatial Consortium. "Simple Feature Access - Part 2: SQL Option". Retrieved 4 November 2021.
- Peuquet, Donna J. (1984). "A conceptual framework and comparison of spatial data models". Cartographica. 21 (4): 66–113. doi:10.3138/D794-N214-221R-23R5.
- Esri. "What is a network dataset?". ArcGIS Pro Documentation. Retrieved 4 November 2021.
- Lo, C.P.; Yeung, Albert K.W. (2002). Concepts and Techniques of Geographic Information Systems. Prentice Hall. p. 81.
- Hägerstrand, Torsten (1970). "What about people in regional science?". Papers of the Regional Science Association. 24 (1): 6–21. doi:10.1007/BF01936872. S2CID 198174673.
- Langran, Gail (1992). Time in Geographic Information Systems. Taylor & Francis.
- Peuquet, Donna J. (1994). "It's about time: a conceptual framework for the representation of temporal dynamics in geographic information systems". Annals of the Association of American Geographers. 84 (3): 441–461. doi:10.1111/j.1467-8306.1994.tb01869.x.
- Gregory, Ian N. (2002). "Time-variant GIS Databases of Changing Historical Administrative Boundaries: A European Comparison". Transactions in GIS. 6 (2): 161–178. doi:10.1111/1467-9671.00103. S2CID 38450649.
- Plewe, Brandon (2019). "A Qualified Assertion Database for the History of Places". International Journal of Humanities and Arts Computing. 13 (1–2): 95–115. doi:10.3366/ijhac.2019.0233. S2CID 207941717.
- Esri. "Fundamentals of netCDF data storage". ArcGIS Pro Documentation. Retrieved 5 November 2021.
- David R. Soller1 and Thomas M. Berg (2003). The National Geologic Map Database Project: Overview and Progress U.S. Geological Survey Open-File Report 03–471.
- D.R. Soller et al. (1999). "Inclusion of digital map products in the National Geologic Map Database". In Soller, D.R., ed., Digital Mapping Techniques '99—Workshop Proceedings. U.S. Geological Survey Open-File Report 99-386, p. 35–38,
Further reading
- B.R. Johnson et al. (1998). Digital geologic map data model. v. 4.3: AASG/USGS Data Model Working Group Report, http://geology.usgs.gov/dm/.
- Soller, D.R., Berg, T.M., and Wahl, Ron (2000). "Developing the National Geologic Map Database, phase 3—An online, "living" database of map information". In Soller, D.R., ed., Digital Mapping Techniques '00—Workshop Proceedings: U.S. Geological Survey Open-File Report 00-325, p. 49–52, http://pubs.usgs.gov/openfile/of00-325/soller4.html.
- Soller, D.R., and Lindquist, Taryn (2000). "Development and public review of the draft "Digital cartographic standard for geologic map symbolization". In Soller, D.R., ed., Digital Mapping Techniques '00—Workshop Proceedings: U.S. Geological Survey Open-File Report 00-325, p. 43–47, http://pubs.usgs.gov/openfile/of00-325/soller3.html.