Gale–Shapley algorithm
In mathematics, economics, and computer science, the Gale–Shapley algorithm (also known as the deferred acceptance algorithm or propose-and-reject algorithm) is an algorithm for finding a solution to the stable matching problem, named for David Gale and Lloyd Shapley. It takes polynomial time, and the time is linear in the size of the input to the algorithm. It is a truthful mechanism from the point of view of the proposing participants, for whom the solution will always be optimal.
Background
The stable matching problem, in its most basic form, takes as input equal numbers of two types of participants (n job applicants and n employers, for example), and an ordering for each participant giving their preference for whom to be matched to among the participants of the other type. A stable matching always exists, and the algorithmic problem solved by the Gale–Shapley algorithm is to find one. A matching is not stable if:
- There is an element A of the first matched set which prefers some given element B of the second matched set over the element to which A is already matched, and
- B also prefers A over the element to which B is already matched.
In other words, a matching is stable when there is no pair (A, B) where both participants prefer each other to their matched partners. If such a pair exists, the matching is not stable, in the sense that the members of this pair would prefer to leave the system and be matched to each other, possibly leaving other participants unmatched.
Solution
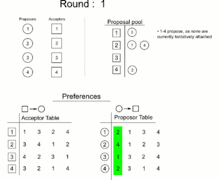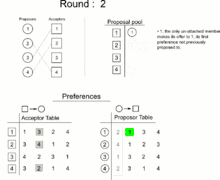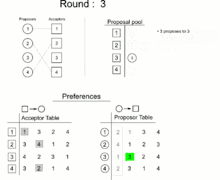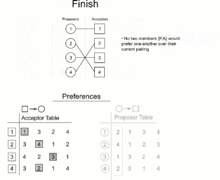
In 1962, David Gale and Lloyd Shapley proved that, for any equal number of participants of each type, it is always possible to find a matching in which all pairs are stable. They presented an algorithm to do so.[1][2] In 1984, Alvin E. Roth observed that essentially the same algorithm had already been in practical use since the early 1950s, in the National Resident Matching Program.[3]
The Gale–Shapley algorithm involves a number of "rounds" (or "iterations"). In terms of job applicants and employers, it can be expressed as follows:
- In each round, any subset of the employers with open job positions makes a job offer to the applicant they prefer, among the ones they have not yet already made an offer to.
- Each applicant who has received an offer evaluates it against their current position (if they have one). If the applicant is not yet employed, or if they receive an offer from an employer they like better than their current employer, they accept the new offer and become matched to the new employer (possibly leaving a previous employer with an open position). Otherwise, they reject the new offer.
- This process is repeated until everyone is employed.
The runtime complexity of this algorithm is where is the number of participants of each type.[4] Since the input preference lists also have size proportional to , the runtime is linear in the input size.
This algorithm guarantees that:
- Everyone gets matched
- At the end, there cannot be an applicant and employer both unmatched. An employer left unmatched at the end of the process must have made an offer to all applicants. But an applicant who receives an offer remains employed for the rest of the process, so there can be no unemployed applicants. Since the numbers of applicants and job openings is equal, there can also be no open positions remaining.
- The matches are stable
- If an applicant X and an employer Y could form an unstable pair, Y would have made an offer to X prior to the offer made by Y to their actual match. But X would have accepted this offer and kept it over the offer they ended up with. Therefore, no such pair is possible.
Algorithm
algorithm stable_matching is
Initialize e ∈ E and a ∈ A to free
while ∃ free employer e who has an applicant a to send an offer to do
a := first applicant on e's list to whom e has not yet sent an offer
if ∃ some pair (e', a) then
if a prefers e to e' then
e' becomes free
(e, a) become matched
end if
else
(e, a) become matched
end if
repeat
Optimality of the solution
The existence of different stable matchings raises the question: which matching is returned by the Gale–Shapley algorithm? Is it the matching better for applicants, for employers, or the intermediate one? As it turns out, the Gale–Shapley algorithm in which employers make offers to applicants yields a stable matching that is the best for all employers and worst for all applicants among all stable matchings.
In a reversed form of the algorithm, each round consists of unemployed applicants writing a single job application to their preferred employer, and the employer either accepting the application (possibly firing an existing employee to do so) or rejecting it. This produces a matching that is best for all applicants and worst for all employers among all stable matchings. These two matchings are the top and bottom elements of the lattice of stable matchings.
In both forms of the algorithm, one group of participants proposes matches, and the other group decides whether to accept or reject each proposal. The matching is always best for the group that makes the propositions, and worst for the group that decides how to handle each proposal.
Strategic considerations
The Gale–Shapley algorithm is a truthful mechanism from the point of view of the proposing side. This means that no proposer can get a better matching by misrepresenting their preferences. Moreover, the Gale–Shapley algorithm is even group-strategy proof for proposers, i.e., no coalition of proposers can coordinate a misrepresentation of their preferences such that all proposers in the coalition are strictly better-off.[5] However, it is possible for some coalition to misrepresent their preferences such that some proposers are better-off, and the others retain the same partner.[6]
The Gale–Shapley algorithm is non-truthful for the non-proposing participants. Each may be able to misrepresent their preferences and get a better match.
Implementation in software packages
- R: The Gale–Shapley algorithm (also referred to as deferred-acceptance algorithm) for the stable marriage and the hospitals/residents problem is available as part of the
matchingMarkets[7][8] andmatchingR[9] packages. - R: Implementation in an R Shiny tool[10] designed for student placement in university programs with limited enrollment (does not use the packages above)
- API: The MatchingTools API provides a free application programming interface for the Gale–Shapley algorithm.[11]
- Python: The Gale–Shapley algorithm is included along with several other well-known matching game algorithms in the
matchinglibrary,[12] andQuantEcon/MatchingMarkets.pypackage[13] includes several others for generalized matching games. - MATLAB: The Gale–Shapley algorithm is implemented in the
assign2DStablefunction that is part of the United States Naval Research Laboratory's free Tracker Component Library.[14]
Recognition
Shapley and Roth were awarded 2012 Nobel Memorial Prize in Economic Sciences "for the theory of stable allocations and the practice of market design"; Gale had died in 2008.[15]
See also
References
- Gale, D.; Shapley, L. S. (1962). "College Admissions and the Stability of Marriage". American Mathematical Monthly. 69 (1): 9–14. doi:10.2307/2312726. JSTOR 2312726. Archived from the original on 2017-09-25. Retrieved 2019-11-20.
- Harry Mairson: "The Stable Marriage Problem", The Brandeis Review 12, 1992 (online).
- Bergstrom, Theodore C. (June 1992). "Review of Two-Sided Matching: A Study in Game-Theoretic Modeling and Analysis by A. E. Roth and M. A. O. Sotomayor". Journal of Economic Literature. 30 (2): 896–898. JSTOR 2727713.
- Iwama, Kazuo; Miyazaki, Shuichi (2008). "A Survey of the Stable Marriage Problem and Its Variants" (PDF). International Conference on Informatics Education and Research for Knowledge-Circulating Society (Icks 2008). pp. 131–136. doi:10.1109/ICKS.2008.7. hdl:2433/226940. ISBN 978-0-7695-3128-1. S2CID 10642344.
- Dubins, L. E.; Freedman, D. A. (1981). "Machiavelli and the Gale–Shapley algorithm". American Mathematical Monthly. 88 (7): 485–494. doi:10.2307/2321753. JSTOR 2321753. MR 0628016.
- Huang, Chien-Chung (2006). "Cheating by men in the Gale-Shapley stable matching algorithm". In Azar, Yossi; Erlebach, Thomas (eds.). Algorithms - ESA 2006, 14th Annual European Symposium, Zurich, Switzerland, September 11-13, 2006, Proceedings. Lecture Notes in Computer Science. Vol. 4168. Springer. pp. 418–431. doi:10.1007/11841036_39. MR 2347162.
- Klein, T. (2015). "Analysis of Stable Matchings in R: Package matchingMarkets" (PDF). Vignette to R Package MatchingMarkets.
- "matchingMarkets: Analysis of Stable Matchings". R Project. 12 January 2020.
- "matchingR: Matching Algorithms in R and C++". R Project. 25 May 2021.
- "Optimal Master Track Allocation". 30 Dec 2017.
- "MatchingTools API".
- Wilde, H.; Knight, V.; Gillard, J. (2020). "Matching: A Python library for solving matching games". Journal of Open Source Software. 5 (48): 2169. Bibcode:2020JOSS....5.2169W. doi:10.21105/joss.02169.
- "matchingMarkets.py". Python package. 27 September 2021.
- "Tracker Component Library". Matlab Repository. Retrieved January 5, 2019.
- "Economics Nobel Honors Perfect Match". Science Mag. Retrieved December 5, 2020.